Đáp án C
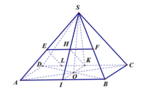
Ta có, CD song song mặt phẳng (SAB) chứa SA nên khoảng cách giữa SA và CD chính là khoảng cách từ CD đến (SAB).
Gọi I, K theo thứ tự là trung điểm AB, CD thì:
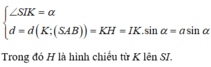
Đáp án C

Ta có, CD song song mặt phẳng (SAB) chứa SA nên khoảng cách giữa SA và CD chính là khoảng cách từ CD đến (SAB).
Gọi I, K theo thứ tự là trung điểm AB, CD thì:
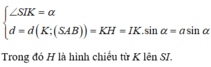
Cho hình chóp tứ giác đều S.ABCD có chiều cao bằng h, góc giữa hai mặt phẳng bằng S A B v à A B C D bằng α Tính thể tích của khối chóp S.ABCD theo h v à α .
A. 3 h 3 4 tan 2 α
B. 4 h 3 3 tan 2 α
C. 8 h 3 3 tan 2 α
D. 3 h 3 8 tan 2 α
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao AH vuông góc với (ABCD). Gọi α là góc giữa BD và (SAD). Tính sin α
A. sin α = 6 4
B. sin α = 1 2
C. sin α = 3 2
D. sin α = 10 4
Cho khối chóp tứ giác đều S.ABCD có thể tích bằng a 3 và đáy ABCD là hình vuông cạnh a. Tính cosα với α là góc giữa mặt bên và mặt đáy
A. cos α = 1 5
B. cos α = 1 3
C. cos α = 1 37
D. cos α = 1 19
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = a , B C = a 3 , S A = a và SA vuông góc với đáy ABCD. Tính sin α , với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng S B C .
A. sin α = 7 8
B. sin α = 3 2
C. sin α = 2 4
D. sin α = 3 5
Cho khối chóp tứ giác đều S.ABCD, gọi α mặt phẳng qua A và vuông góc SC.
Biết rằng diện tích thiết diện tạo bởi α là hình chóp bằng nửa diện tích đáy ABCD. Tính
góc φ tạo bởi cạnh bên SC và mặt đáy.
A. φ = arcsin 1 + 33 8
B. φ = arcsin 33 − 1 8
C. φ = arcsin 1 + 29 8
D. φ = arcsin 29 − 1 8
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với đáy. Biết rằng khoảng cách từ điểm A đến mặt phẳng (SBC) bằng a. Xét góc α thảy đổi là số đo của góc giữa đường thẳng SB và mặt phẳng đáy. Tính cos α sao cho thể tích của hình chóp S.ABCD đạt giá trị nhỏ nhất
A. cos α = 3 6
B. cos α = 6 3
C. cos α = 3 3
D. cos α = 6 6
Cho hình chóp A.BCD có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A trên mặt phẳng đáy là trung điểm H của CD. Cắt hình chóp bởi mặt phẳng ( α ) song song với AB và CD. Tính diện tích S của thiết diện thu được, biết d ( B , ( α ) ) = a 2 , A B = a 2
A. S = 4 a 15 ( a 15 + 2 a 2 )
B. S = 4 a 15 ( a 15 + a 2 )
C. S = 4 a 15 ( a 15 - 2 a 2 )
D. S = 4 a 15 ( a 15 - a 2 )
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, S A ⊥ ( A B C D ) và S A = 3 . Gọi α là góc tạo bởi giữa đường thẳng SB và mặt phẳng (SAC), khi đó α thỏa mãn hệ thức nào sau đây?
A. cos α = 2 8
B. sin α = 2 8
C. sin α = 2 4
D. cos α = 2 4
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, góc BAD = 600 , SA=SB=SD= a 3 2 . Gọi α là góc giữa đường thẳng SD và mặt phẳng (SBC). Giá trị sin α bằng
A. 1 3
B. 2 3
C. 5 3
D. 2 2 3