Phương pháp:
- Gắn hệ tọa độ Oxyz với O là tâm hình vuông đáy,

- Xác định tọa độ các điểm cần thiết và tính khoảng cách.
Cách giải:
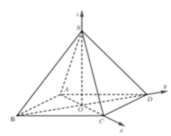
Gắn hệ trục tọa độ như hình vẽ, giả sử SO = b ta có:
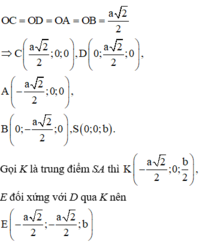

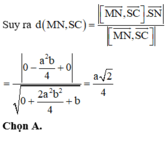
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Phương pháp:
- Gắn hệ tọa độ Oxyz với O là tâm hình vuông đáy,

- Xác định tọa độ các điểm cần thiết và tính khoảng cách.
Cách giải:

Gắn hệ trục tọa độ như hình vẽ, giả sử SO = b ta có:
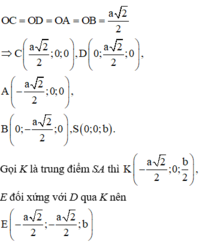


Cho hình chóp tứ giác đều S.ABCD đáy ABCD là hình vuông, E là điểm đối xứng của D qua trung điểm của SA. Gọi M, N lần lượt là trung điểm của AE và BC. Góc giữa hai đường thẳng MN và BD bằng:
A. 90 o
B. 60 o
C. 45 o
D. 75 o
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông, E là điểm đối xứng của D qua trung điểm SA. Gọi M, N lần lượt là trung điểm của AE và BC. Góc giữa hai đường thẳng MN và BD bằng
A. 60 0 .
B. 90 0 .
C. 45 0 .
D. 75 0 .
Cho hình chóp tứ giác đều S.ABCD. Gọi E là điểm đối xứng của D qua trung điểm của SA. Gọi M, N lần lượt là trung điểm của AE và BC. Tính góc giữa hai đường thẳng MN và BD.
A. 30 °
B. 45 °
C. 60 °
D. 90 °
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc 60 ° . Gọi M là điểm đối xứng với C qua D; N là trung điểm của SC, mặt phẳng ( BMN) chia khối chóp S.ABCD thành hai phân. Tính tỉ số thể tích giữa hai phần đó
A. 1 5
B. 7 3 .
C. 1 7
D. 7 5
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Gọi M, N lần lượt là trung điểm của SA và BC. Biết góc giữa MN và mặt phẳng (ABCD) bằng 60 0 . Khoảng cách giữa hai đường thẳng BC và DM là:
A. a 15 62
B. a 30 31
C. a 15 68
D. a 15 17
Cho hình chóp tứ giá đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc 60 ° . Gọi M là điểm đối xứng của C qua D, N là trung điểm SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai phần. Tỉ số thể tích giữa hai phần (phần lớn trên phần bé) bằng:
A. 7 5
B. 1 7
C. 7 3
D. 6 5
Cho khối chóp tứ giác đều S.ABCD có dạng đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 ° . Gọi M là điểm đối xứng với C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện H 1 và H 2 , trong đó H 1 chứa điểm C. Thể tích của khối H 1 là:
A. 7 6 a 3 72
B. 5 6 a 3 72
C. 5 6 a 3 36
D. 7 6 a 3 36
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 ° Gọi M là điểm đối xứng vưới C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện H 1 và H 2 trong đó H 1 chứa điểm C. Thể tích của khối là
A. 7 6 a 3 72
B. 5 6 a 3 72
C. 5 6 a 3 36
D. 7 6 a 3 36
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp đáy một góc 60 ∘ . Gọi M là điểm đối xứng với C qua D, N là trung điểm SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện. Tính thể tích V
A. V = 7 6 a 3 36
B. V = 7 6 a 3 72
C. V = 5 6 a 3 72
D. V = 5 6 a 3 36