Chọn đáp án D

Gọi I là trung điểm của SA. Khi đó I cũng là trung điểm của ED.


Vậy góc giữa hai đường thẳng MN và BD bằng 90 °
Chọn đáp án D

Gọi I là trung điểm của SA. Khi đó I cũng là trung điểm của ED.


Vậy góc giữa hai đường thẳng MN và BD bằng 90 °
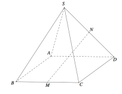
Cho hình chóp tứ giác đều S.ABCD đáy ABCD là hình vuông, E là điểm đối xứng của D qua trung điểm của SA. Gọi M, N lần lượt là trung điểm của AE và BC. Góc giữa hai đường thẳng MN và BD bằng:
A. 90 o
B. 60 o
C. 45 o
D. 75 o
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông, E là điểm đối xứng của D qua trung điểm SA. Gọi M, N lần lượt là trung điểm của AE và BC. Góc giữa hai đường thẳng MN và BD bằng
A. 60 0 .
B. 90 0 .
C. 45 0 .
D. 75 0 .
Cho hình chóp tứ giác đều S.ABCD cạnh đáy bằng a. Gọi E là điểm đối xứng với D qua trung điểm của S A; M, N lần lượt là trung điểm AE , BC. Khoảng cách giữa hai đường thẳng MN, SC bằng
A. a 2 4 .
B. a 2 2 .
C. a 3 4 .
D. a 3 2 .
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a tâm O. Gọi M, N lần lượt là trung điểm của SA và BC. Góc giữa đường thẳng MN và mặt phẳng (ABCD) bằng 60 ° . Tính cosin góc giữa đường thẳng và mặt phẳng (SBD)
A. 41 41
B. 5 5
C. 2 5 5
D. 2 41 41
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Gọi M, N lần lượt là trung điểm của SA và BC. Biết góc giữa MN và mặt phẳng (ABCD) bằng 60 0 . Khoảng cách giữa hai đường thẳng BC và DM là:
A. a 15 62
B. a 30 31
C. a 15 68
D. a 15 17
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc 60 ° . Gọi M là điểm đối xứng với C qua D; N là trung điểm của SC, mặt phẳng ( BMN) chia khối chóp S.ABCD thành hai phân. Tính tỉ số thể tích giữa hai phần đó
A. 1 5
B. 7 3 .
C. 1 7
D. 7 5
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M,N lần lượt là trung điểm các cạnh BC,SD. Góc giữa hai đường thẳng MN và AB bằng
A. 30 °
B. 45 °
C. 60 °
D. 36 °
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 ° Gọi M là điểm đối xứng vưới C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện H 1 và H 2 trong đó H 1 chứa điểm C. Thể tích của khối là
A. 7 6 a 3 72
B. 5 6 a 3 72
C. 5 6 a 3 36
D. 7 6 a 3 36
Cho khối chóp tứ giác đều S.ABCD có dạng đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 ° . Gọi M là điểm đối xứng với C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện H 1 và H 2 , trong đó H 1 chứa điểm C. Thể tích của khối H 1 là:
A. 7 6 a 3 72
B. 5 6 a 3 72
C. 5 6 a 3 36
D. 7 6 a 3 36