Đáp án C.
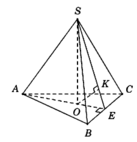
Gọi O là tâm của tam giác đều ABC.
Do hình chóp S.ABC đều nên suy ra S O ⊥ ( A B C ) .
Ta có d A ; S B C = 3 × d O ; S B C .
Gọi E là trung điểm BC; Kẻ O K ⊥ S E ⇒ d O ; S B C = O K .
Tính được S O = S A 2 - O A 2 = 2 6 3 và O E = 1 3 A E = a 3 6 .
Tám giác vuông SOE, có O K = S O . O E S O 2 + O E 2 = 2 a 22 33 .
Vậy d = d 1 + d 2 = 4 d 2 = 8 a 22 22 .



