Đáp án A
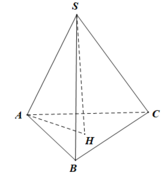
Gọi H là tâm của tam giác đều A B C ⇒ S H ⊥ A B C
S A ; A B C = S A ; H A = ∠ S A H = φ A H = 2 3 . a 3 2 = a 3 3 S H = A H . tan φ = a 3 3 tan φ V S . A B C = 1 3 . S H . S A B C = 1 3 . a 3 3 tan φ . a 2 3 4 = a 3 tan φ 12
Đáp án A

Gọi H là tâm của tam giác đều A B C ⇒ S H ⊥ A B C
S A ; A B C = S A ; H A = ∠ S A H = φ A H = 2 3 . a 3 2 = a 3 3 S H = A H . tan φ = a 3 3 tan φ V S . A B C = 1 3 . S H . S A B C = 1 3 . a 3 3 tan φ . a 2 3 4 = a 3 tan φ 12
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAB là tam giác đều và (SAB) vuông góc với (ABCD). Tính cos φ với φ là góc tạo bởi (SAC) và (SCD).
A. 2 7
B. 6 7
C. 3 7
D. 5 7
Cho khối chóp tứ giác đều S.ABCD, gọi α mặt phẳng qua A và vuông góc SC.
Biết rằng diện tích thiết diện tạo bởi α là hình chóp bằng nửa diện tích đáy ABCD. Tính
góc φ tạo bởi cạnh bên SC và mặt đáy.
A. φ = arcsin 1 + 33 8
B. φ = arcsin 33 − 1 8
C. φ = arcsin 1 + 29 8
D. φ = arcsin 29 − 1 8
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 3a. Gọi φ là góc giữa cạnh bên và mặt phẳng đáy. Tính tan φ .
A. tan φ = 3 2
B. tan φ = 2 3
C. tan φ = 2 3 3
D. tan φ = 2
Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a; cạnh bên trùng với đáy một góc φ sao cho A’ có hình chiếu xuống mặt phẳng ( ABC ) trùng với trọng tâm của ∆ A B C . Tính thể tích khối lăng trụ.
A. a 3 4 tan φ
B. a 3 4 c o t φ
C. a 3 12 tan φ
D. a 3 12 c o t φ
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên SA vuông góc với mặt đáy (ABC) và S A = a 3 . Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABC). Mệnh đề nào sau đây đúng?
A. φ = 30 °
B. φ = 60 °
C. sin φ = 5 5
D. sin φ = 2 5 5
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật có AB = a. Biết SA = a và vuông góc với đáy. Góc giữa mặt phẳng (SBC) và (SCD) bằng φ , với cos φ = 2 5 . Tính theo a thể tích của khối chóp S.ABCD
A. 4 3 a 3
B. 2 3 a 3
C. 2 a 3
D. a 3 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a cạnh bên SA vuông góc
mặt đáy và SA = a . Gọi φ là góc tạo bởi SB và mặt (ABCD). Xác định cot φ
A. cot φ = 2
B. cot φ = 1 2
C. cot φ = 2 2
D. cot φ = 2 4
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy, diện tích tam giác SAB bằng a 2 . Gọi φ là góc giữa hai mặt phẳng (SCD) và (ABCD). Tính tan φ
tan φ
B. tan φ = 1
C. tan φ = 2
D. tan φ = 3
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a, gọi φ là góc giữa hai mặt phẳng S A B v à C S D . Tính cos φ
A. cos φ = 1 2
B. cos φ = 1 6
C. cos φ = 1 3
D. cos φ = 1 4