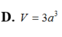Chọn B.
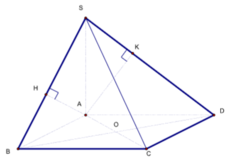
+ Gọi AD = x (x > 0)
+ Kẻ![]() dễ dàng chứng minh được
dễ dàng chứng minh được ![]()
![]()
Trong tam giác SBC ta có
![]()
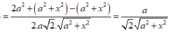
Trong tam giác SAD có ![]()
Xét tam giác AHK có
![]()
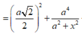
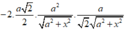
![]()
Xét tam giác AHK có
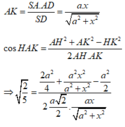
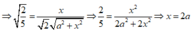
Vậy ![]()
Chọn B.

+ Gọi AD = x (x > 0)
+ Kẻ![]() dễ dàng chứng minh được
dễ dàng chứng minh được ![]()
![]()
Trong tam giác SBC ta có
![]()
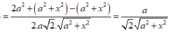
Trong tam giác SAD có ![]()
Xét tam giác AHK có
![]()
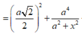
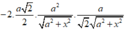
![]()
Xét tam giác AHK có
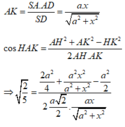
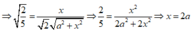
Vậy ![]()
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, BC = 2a, cạnh bên SA vuông góc với mặt đáy, SA = a. Gọi H là hình chiếu của a trên SB, tính thể tích khối chóp H.ABCD theo a và côsin của góc giữa 2 mặt phẳng (SBC) và (SCD)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, BC= a 3 , SA = a và SA vuông góc với đáy ABCD. Tính sin α , với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC).
A. sin α = 7 8
B. sin α = 3 2
C. sin α = 2 4
D. sin α = 3 5
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, BC = a 3 ,SA = a và SA vuông góc với đáy ABCD. Tính sinα, với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC)
A . sin α = 7 8
B . sin α = 3 2
C . sin α = 2 4
D . sin α = 3 5
Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật với AB = a, BC = a 3 . Cạnh bên SA vuông góc với đáy và đường thẳng SC tạo với mặt phẳng (SAB) một góc 30 độ. Tính thể tích V của khối chóp S.ABCD theo a.
A. V = 2 6 a 3 3
B. V = 2 a 3 3
C. V = 3 a 3
D. V = 3 a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, tam giác SAD vuông tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Biết AB = a, SA = 2SD, mặt phẳng (SBC) tạo với mặt phẳng đáy một góc 60 ° . Thể tích của khối chóp S.ABCD bằng:
A. 15 a 3 2
B. 3 a 3 2
C. 5 a 3 2
D. 5 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với đáy AB=a, AD=a 2 , SA=a 3 . Số đo của góc giữa SC và mặt phẳng (ABCD) bằng
A. 300
B. 450
C. 600
D. 750
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB= a 3 và AD=a. Đường thẳng SA vuông góc với mặt phẳng đáy và SA=a. Thể tích khối cầu ngoại tiếp hình chóp S.BCD bằng
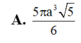
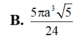
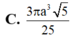
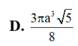
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy (ABCD), AB = a, AD = 2. Góc giữa cạnh bên SB và mặt phẳng (ABCD) bằng 45°. Thể tích hình chóp S.ABCD bằng
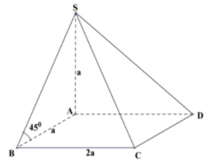
A. 6 a 3 18
B. 2 2 a 3 3
C. a 3 3
D. 2 a 3 3
Cho khối chóp S . A B C D có đáy là hình chữ nhật, A B = a , A D = a 3 , S A vuông góc với đáy và mặt phẳng ( S B C ) tạo với đáy một góc 60 0 . Tính thể tích V của khối chóp S . A B C D
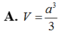
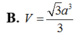
![]()