Question

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, BC = 2a, cạnh bên SA vuông góc với mặt đáy, SA = a. Gọi H là hình chiếu của a trên SB, tính thể tích khối chóp H.ABCD theo a và côsin  của góc giữa 2 mặt phẳng (SBC) và (SCD)

Answer 1

Ai làm cho 10 coin;-;

Answer 2

s lại đưa 12?

Answer 3

hình t k vẽ chụp mài đc tại máy t hết pin , h m uy tín 100 coin thì t lm đc

Answer 4

lm xong k thấy 100 coin t phốt réng chịu:>

Answer 5

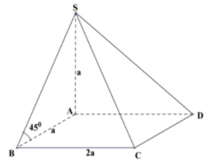
Kẻ HE//SA \(\left(E\in AB\right)\) => HE ⊥ ( ABCD)

Trong ΔSAB có \(AB^2=BH.SB\Rightarrow\dfrac{BH}{SB}=\dfrac{AB^2}{SB^2}=\dfrac{1}{2}=\dfrac{HE}{SA}\Rightarrow HE=\dfrac{a}{2}\)

\(S_{ACD}=\dfrac{1}{2}AD.CD=a^2\Rightarrow\) thể tích H.ACD là \(V_{H.ACD}=\dfrac{1}{3}HE.S_{ACD}=\dfrac{a^3}{6}\)

SA ⊥ ( ABCD) => SA ⊥ BC mà BC ⊥ AB nên BC ⊥ (SAB) 

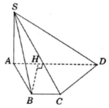
=> BC ⊥ HA mà HA ⊥ SB nên HA ⊥ (SBC)

tương tự : gọi K là hình chiếu của A trên SD thì AK ⊥ ( SCD) , do vậy góc giữa hai mặt phẳng ( SBC) và (SCD) là góc giữa AH và AK.

Trong Δ vuông SAB có : \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{SA^2}\Rightarrow AH=\dfrac{a\sqrt{2}}{2}\)

\(SA^2=SH.SB\Rightarrow SH=\dfrac{a\sqrt{2}}{2}\)

tương tự : \(AK=\dfrac{2a}{\sqrt{5}};SK=\dfrac{a}{\sqrt{5}}\)

cos góc BSD = \(\dfrac{SB^2+SD^2-BD^2}{2.SB.SD}=\dfrac{SH^2+SK^2-HK^2}{2.SH.SK}\Rightarrow HK^2=\dfrac{a^2}{2}\)

Trong ΔAHK có cos góc AHK =\(\dfrac{AH^2+AK^2-HK^2}{2.AH.K}=\dfrac{\sqrt{10}}{5}>0\)

=> cos tất cả ((SBC),(SCD)) = \(\dfrac{\sqrt{10}}{5}\)