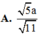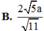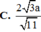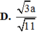Đáp án C
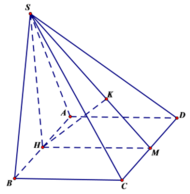
Gọi M là trung điểm của CD. Kẻ HK vuông góc với SM.
Ta có:

Mặt khác ta có HK ⊥ SM
Suy ra HK ⊥ (SCD)
Vậy ![]()
Xét tam giác BHC vuông tại B, ta có:
![]()
![]()
Xét tam giác SHM vuông tại H, ta có:
![]()

Đáp án C

Gọi M là trung điểm của CD. Kẻ HK vuông góc với SM.
Ta có:

Mặt khác ta có HK ⊥ SM
Suy ra HK ⊥ (SCD)
Vậy ![]()
Xét tam giác BHC vuông tại B, ta có:
![]()
![]()
Xét tam giác SHM vuông tại H, ta có:
![]()

Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a. Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AB, SC tạo với đáy một góc bằng 45º. Khoảng cách từ điểm A tới mặt phẳng (SCD).
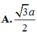
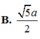
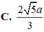
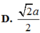
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm H thuộc cạnh AB sao cho HB = 2HA. Cạnh SC tạo với mặt phẳng đáy (ABCD) một góc bằng 60 0 . Khoảng cách từ trung điểm K của HC đến mặt phẳng (SCD) là
A . a 13 2
B . a 13 4
C . a 13
D . a 13 8
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB =a, AD = 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45 0 .Gọi M là trung điểm của SD. Tính theo a khoảng cách d từ điểm M đến mặt phẳng (SAC)
A. d = a 1315 89
B. d = a 1513 89
C. d = 2 a 1315 89
D. d = 2 a 1513 89
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB =a, AD = 2a Cạnh bên SA vuông góc với mặt phẳng đáy và cạnh bên SC tạo với đáy một góc 60 o Gọi M, N là trung điểm các cạnh bên SA và SB Khoảng cách từ điểm S đến mặt phẳng (DMN) bằng
A. 2 a 465 31
B. a 31 31
C. a 60 31
D. 2 a 5 31
cho hình chóp SABCD đáy ABCD là hình chữ nhật AB= a ,AD=2a,SA=SB=SC=SD=2a gọi O là giao điểm của AC và BD
a chứng minh mặt phẳng SAC vuông góc với mặt phẳng ABCD
b tính khoảng cách từ O->mặt phẳng SCD
c gọi M,N lần lượt là trung điểm của các cạnh SA và BC tính sin góc MN,CSBD
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh A. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm I thuộc đoạn AB sao cho BI = 2AI. Góc giữa mặt bên (SCD) và mặt đáy (ABCD) bằng 60 0 . Tính khoảng cách giữa hai đường thẳng AD và SC.
A . 93 31 a
B . 3 93 31 a
C . 93 31
D . 3 93 31 a
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, AB =a 3 vuông góc với mặt phẳng đáy. Biết rằng khoảng cách giữa BD và SC bằng a 3 2 . Tính khoảng cách d từ B đến mặt phẳng (SCD)
A. a 6 2
B. a 6 2
C. a 2
D. 2 a 3 3
Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật,AB=a, AD=2a. Đường cao SA bằng 2a. Khoảng cách từ trung điểm M của SB đến mặt phẳng (SCD) bằng
![]()
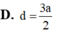
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, AB = 2a, AC = 2a. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của cạnh AB. Cạnh bên SC hợp với đáy (ABC) một góc 45 ° Khoảng cách từ A đến mặt phẳng (SBC) là