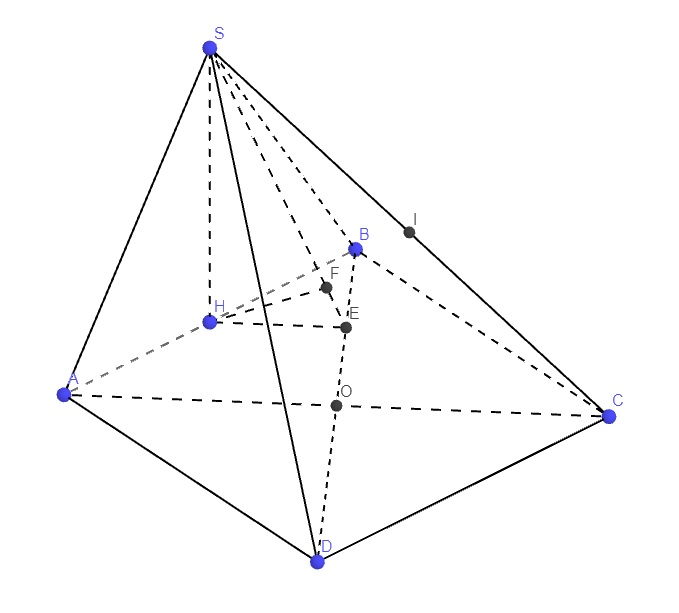
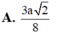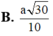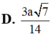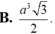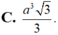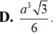Gọi O là tâm đáy, H là trung điểm AB \(\Rightarrow SH\perp\left(ABCD\right)\)
\(IS=\dfrac{1}{2}CS\Rightarrow d\left(I;\left(SBD\right)\right)=\dfrac{1}{2}d\left(C;\left(SBD\right)\right)\)
\(\left\{{}\begin{matrix}AC\cap\left(SBD\right)=O\\CO=AO\end{matrix}\right.\) \(\Rightarrow d\left(C;\left(SBD\right)\right)=d\left(A;\left(SBD\right)\right)\)
\(\left\{{}\begin{matrix}AH\cap\left(SBD\right)=B\\AB=2HB\end{matrix}\right.\) \(\Rightarrow d\left(A;\left(SBD\right)\right)=2d\left(H;\left(SBD\right)\right)\)
\(\Rightarrow d\left(I;\left(SBD\right)\right)=d\left(H;\left(SBD\right)\right)\)
Từ H kẻ HE vuông BD và HF vuông SE
\(\Rightarrow HF\perp\left(SBD\right)\Rightarrow HF=d\left(H;\left(SBD\right)\right)\)
\(SH=\dfrac{a\sqrt{3}}{2}\); \(HE=HB.sin\widehat{HBE}=\dfrac{a}{2}.sin45^0=\dfrac{a\sqrt{2}}{4}\)
\(\Rightarrow HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\)