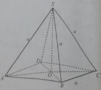
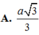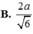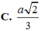Hình bạn tự vẽ nhé ;)
Gọi O là tâm của ABCD thì có O là trung điểm AC,BD, \(OB=OD=\dfrac{BD}{2}=\dfrac{a}{\sqrt{2}}\) và \(BD\perp AC\).
Do SA vuông (ABCD) nên tam giác ASD và ASB vuông tại A, suy ra \(SD=SB=\sqrt{a^2+a^2}=a\sqrt{2}\), suy ra tam giác SBD cân tại S, mà O là trung điểm BD nên SO vuông BD.
Ta có BD là giao tuyến của (SBD) và (ABCD), đồng thời \(OA\perp BD\) ; \(OS\perp BD\), nên \(\left(\left(SBD\right),\left(ABCD\right)\right)=\widehat{SOA}\).
Có \(OS=\sqrt{SD^2-OD^2}=\sqrt{2a^2-\dfrac{a^2}{2}}=\dfrac{a\sqrt{6}}{2}\)
\(\Rightarrow cos\widehat{SOA}=\dfrac{OS^2+OA^2-AS^2}{2OS.OA}=\dfrac{\dfrac{3a^2}{2}+\dfrac{a^2}{2}-a^2}{2.\dfrac{a}{\sqrt{2}}.a}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{SOA}=45^0\)
a đúng b sai