Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB và AB 2CD. Gọi I, J, K lần lượt là ba điểm trên các cạnh SA; AB; BC. Gọi F là giao điểm của SD và (IJK). Tính tỉ số
F
S
F
D
A. 1 B. 2 C.
1
2
D.
1
3
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB và AB= 2CD. Gọi I, J, K lần lượt là ba điểm trên các cạnh SA; AB; BC. Gọi F là giao điểm của SD và (IJK). Tính tỉ số F S F D
A. 1
B. 2
C. 1 2
D. 1 3
Cho hình chóp S.ABCD có đáy là hình thang; đáy lớn AB. Gọi I; J; K lần lượt là 3 điểm trên SA; AB; BC. Gọi E là giao điểm của AK và BD; F là giao điểm của IK và SE; M là giao điểm của JK và BD. Tìm giao điểm của (IJK) và SD A. là giao điểm của SD và MF B. Là giao điểm của SD và ME C. Là giao điểm của SD và EF D. là giao điểm của SD và EK
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang; đáy lớn AB. Gọi I; J; K lần lượt là 3 điểm trên SA; AB; BC. Gọi E là giao điểm của AK và BD; F là giao điểm của IK và SE; M là giao điểm của JK và BD. Tìm giao điểm của (IJK) và SD
A. là giao điểm của SD và MF
B. Là giao điểm của SD và ME
C. Là giao điểm của SD và EF
D. là giao điểm của SD và EK
cho hình chóp s.abcd có đáy abcd là hình bình hành. gọi i,j,k theo thứ tự là trung điểm của các cạnh ab, cd và sa. a) tìm giao tuyến của hai mp (SAB)và(SCD) b) CM: IJ // (SCD) c) tìm giao điểm của đường thẳng SD với mp(IJK)
Cho hình chóp S.ABCD có đáy ABCD là hình thang ( đáy lớn AB). Gọi I,J lần lượt là trung điểm của AD và BC, K là điểm trên cạnh SB sao cho SK=2/3SB
a. Tìm giao tuyến của (SAB) và (IJK)
b. Tìm thiết diện của ( IJK) với hình chóp S.ABCD. Tìm điều kiện để thiết diện là hình bình hành
Cho hình chóp S.ABCD có đáy là hình thang với các cạnh đáy là AB và CD. Gọi I ,J lần lượt là trung điểm của AD và BC, G là trọng tâm của tam giác SAB. Tìm giao tuyến của hai mặt phẳng (SAB) và (IJG).
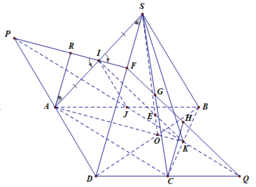
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, hai điểm M, N lần lượt là trung điểm của SB, SD; điểm P thuộc SC và không là trung điểm của SC. Gọi E là giao điểm của SO và MN; Q là giao điểm của SA và PE. Gọi F, G, H lần lượt là giao điểm của QM và AB, QP và AC, QN và AD. Tìm khẳng định đúng? A. F nằm giữa G và H B. 3 điểm F; G; H không thẳng hàng C. G nằm giữa F và H D. Tất cả sai
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, hai điểm M, N lần lượt là trung điểm của SB, SD; điểm P thuộc SC và không là trung điểm của SC. Gọi E là giao điểm của SO và MN; Q là giao điểm của SA và PE. Gọi F, G, H lần lượt là giao điểm của QM và AB, QP và AC, QN và AD. Tìm khẳng định đúng?
A. F nằm giữa G và H
B. 3 điểm F; G; H không thẳng hàng
C. G nằm giữa F và H
D. Tất cả sai
Cho hình chóp S. ABCD có đáy là hình thang; đáy lớn AB. Gọi I; J; K lần lượt là 3 điểm trên SA; AB; BC. Gọi E là giao điểm của AK và BD. Tìm giao điểm của IK và (SBD)
A. Là giao điểm của IJ và SE
B. là giao điểm của IA và SE
C. là giao điểm của IK và SE
D. Là giao điểm của IE và SK
Bt2: cho hình chóp S.ABCD đáy là tứ giác lồi có AB>CD .gọi M,N lần lượt là trung điểm của cạnh SA và SD .a) tìm giao tuyến (SAB) và (SCD).b) tìm giao tuyến của (MNC) và (ABCD).c)tìm giao điểm của MN và (ABN).d) tìm thiết diện của hình chóp vs mp (BMN)
Cho hình chóp S.ABCD có đáy ABCD là hình thang(hai cạnh đáy là AB,CD). Gọi I,J lần lượt là trung điểm của các cạnh AD,BC và G là trọng tâm của ΔSAB. Tìm k để AB=k*CD để thiết diện của mặt phẳng (GIJ) với hình chóp S.ABCD là hình bình hành