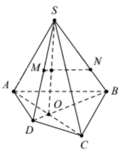
Cho hình chóp S.ABCD có đáy không là hình thàng. Trên SC lấy điểm M. Gọi N là giao điểm của của SD và ( AMB). Tìm mện đề đúng?
A. 3 đường thẳng AB; CD; MN đôi một song song
B. 3 đường thẳng AB; CD; MN đôi một cắt nhau
C. 3 đường thẳng AB; CD; MN đồng quy
D. 3 đường thẳng AB; CD; MN cùng thuộc 1 mặt phẳng
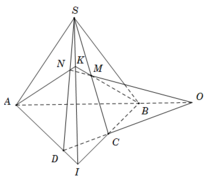
Gọi giao điểm của AD và BC là I Trong mặt phẳng (SBC) , gọi K là giao điểm của BM và SI. Trong mặt phẳng (SAD) , gọi N là giao điểm AK và SD.
Khi đó N là giao điểm của đường thẳng SD với mặt phẳng (AMB).
Gọi giao điểm của AB và CD là O. Suy ra
+ O thuộc ( AMB).
+ O thuộc CD mà C D ⊂ S C D suy ra O thuộc ( SCD).
Do đó O ∈ A M B ∩ S C D (1)
Mà giao tuyến của (AMB) và ( SCD) là MN (2)
Từ (1) và (2) , suy ra O thuộc MN.
Vậy ba đường thẳng AB; CD; MN đồng quy.
Chọn C.