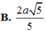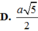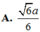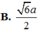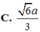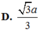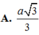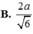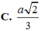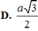Question

cho hình chóp S.ABCD có đáy hình vuông ABCD cạnh a, SA vuông (ABCD), SA = 2a

 a) tính d(SA,BC)

b) tính d(AB,SD)

Answer 1

a.

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\\AB\perp BC\left(gt\right)\end{matrix}\right.\)

\(\Rightarrow AB\) là đường vuông góc chung của SA và BC

\(\Rightarrow d\left(SA,BC\right)=AB=a\)

b.

Từ A kẻ \(AH\perp SH\)

\(\left\{{}\begin{matrix}SA\perp AB\\AB\perp AD\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\Rightarrow AB\perp AH\)

\(\Rightarrow AH=d\left(AB,SD\right)\)

Hệ thức lượng: \(AH=\dfrac{SA.AD}{\sqrt{SA^2+AD^2}}=\dfrac{2a\sqrt{3}}{3}\)