Đáp án B
Phương pháp:
Suy luận từng đáp án, sử dụng phương pháp chứng minh đường thẳng vuông góc với mặt phẳng: Một đường thẳng vuông góc với mặt phẳng khi nó vuông góc với hai đường thẳng cắt nhau trong mặt phẳng đó.

Đáp án B
Phương pháp:

Suy luận từng đáp án, sử dụng phương pháp chứng minh đường thẳng vuông góc với mặt phẳng: Một đường thẳng vuông góc với mặt phẳng khi nó vuông góc với hai đường thẳng cắt nhau trong mặt phẳng đó.

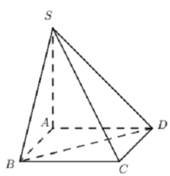
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB cân tại S có S A = S B = 2 a nằm trong mặt phẳng vuông góc với đáy ABCD. Gọi α là góc giữa SD và mặt phẳng đáy (ABCD). Mệnh đề nào sau đây đúng?
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và S A ⊥ A B C D . Gọi M, N, P lần lượt là trung điểm AB, BC và SB. Mệnh đề nào sau đây là sai?
A. M N P / / S A C
B. B D ⊥ M N P
C. Góc giữa SC và BD là 60°
D. B C ⊥ M P
Cho hình chóp S.ABCD có đáy là hình vuông, cạnh bên SA vuông góc với đáy (ABCD). Khẳng định nào sau đây là sai?
A. CD ⊥ (SBC)
B. SA ⊥ (ABC)
C. BC ⊥ (SAB)
D. BD ⊥ (SAC)
Cho hình chóp S.ABCD, tứ giác ABCD đáy là hình thang vuông tại A và B, S vuông góc với mặt phẳng (ABCD). Biết AB=2CD=2AD. Mệnh đề nào sau đây sai?
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, ABC = 60 0 . Hai mặt bên (SAD) và (SAB) cùng vuông góc với đáy (ABCD) . Cạnh SB=a 2 . Mệnh đề nào dưới đây sai?
A. S A B C D = a 2 3 2
B. SC=a 2
C. (SAC ) ⊥ (SBD).
D. V S . A B C D = 5 3 a 3 12
Cho hình chóp S.ABCD có đáy là hình thoi và SA=SC. Mặt phẳng (ABCD) vuông góc với mặt phẳng nào sau đây?
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc với (ABCD). Hình chóp này có mặt đối xứng nào?
A. Không có
B. (SAB)
C. (SAC)
D. (SAD)
Cho khối chóp S . A B C D có đáy A B C D là hình vuông cạnh a . Biết S A vuông góc với đáy A B C D và S A = a 6 . Thể tích khối chóp S . A B C D là
A. a 3 4
B. a 3 3
C. a 3 3 3
D. a 3 2 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=3a và SA vuông góc với mặt phẳng đáy. Tính thể tích khối chóp S.ABCD.
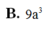
![]()
![]()