Các câu hỏi tương tự
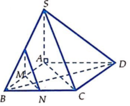
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AB BC a, AD 2a. Biết SA vuông góc với đáy (ABCD) và SA a. Gọi M, N lần lượt là trung điểm SB, CD. Tính sin góc giữa đường thẳng MN và mặt phẳng (SAC). A.
5
5
B.
55
10
C.
3
5
10
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AB = BC = a, AD = 2a. Biết SA vuông góc với đáy (ABCD) và SA = a. Gọi M, N lần lượt là trung điểm SB, CD. Tính sin góc giữa đường thẳng MN và mặt phẳng (SAC).
A. 5 5
B. 55 10
C. 3 5 10
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, ABBCa, AD2a, SA vuông góc với mặt đáy (ABCD), SAa. Gọi M, N lần lượt là trung điểm của SB, CD. Tính cosin của góc giữa đường thẳng MN và (SAC).
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB=BC=a, AD=2a, SA vuông góc với mặt đáy (ABCD), SA=a. Gọi M, N lần lượt là trung điểm của SB, CD. Tính cosin của góc giữa đường thẳng MN và (SAC).
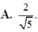
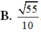
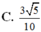
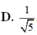
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, biết SC
a
3
. Gọi M, N, P, Q lần lượt là trung điểm các cạnh SB, SD, CD, BC. Tính thể tích khối chóp AMNPQ A.
a
3
3
B.
a
3
4
C.
a
3...
Đọc tiếp
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, biết SC = a 3 . Gọi M, N, P, Q lần lượt là trung điểm các cạnh SB, SD, CD, BC. Tính thể tích khối chóp AMNPQ
A. a 3 3
B. a 3 4
C. a 3 8
D. a 3 12
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy, SA = AC. Mặt phẳng qua A vuông góc với SC cắt SB, SC, SD lần lượt tại B', C', D'. Tỉ số giữa thể tích hình chóp S.A'B'C'D' và thể tích hình chóp S.ABCD là:
A. 1/6 B. 1/4
C. 1/3 D. 1/2
Cho hình chóp S.ABCD có SA ^ (ABC), AB 1, AC 2 và
B
A
C
^
60
∘
. Gọi M, N lần lượt là hình chiếu của A trên SB, SC. Tính bán kính R của mặt cầu đi qua các điểm A, B, C, M, N.
Đọc tiếp
Cho hình chóp S.ABCD có SA ^ (ABC), AB = 1, AC = 2 và B A C ^ = 60 ∘ .
Gọi M, N lần lượt là hình chiếu của A trên SB, SC. Tính bán kính R của
mặt cầu đi qua các điểm A, B, C, M, N.
![]()
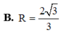
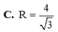
![]()
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Gọi M, N lần lượt là trung điểm của AB và AD, H là giao điểm của MD và NC. Biết rằng SH là đường cao của hình chóp đã cho và cạnh SC tạo với đáy hình chóp đó một góc bằng 60 ° . Tính khoảng cách giữa DM và SC.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,
B
A
D
^
60
°
và SA vuông góc với mặt phẳng (ABCD). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng
45
°
. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích
V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 ° và SA vuông góc với mặt phẳng (ABCD). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng 45 ° . Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V 1 , khối đa diện còn lại có thể tích V 2 (tham khảo hình vẽ bên).
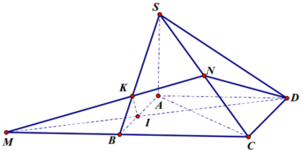
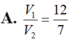
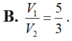
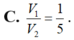
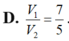
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông, E là điểm đối xứng của D qua trung điểm SA. Gọi M, N lần lượt là trung điểm của AE và BC. Góc giữa hai đường thẳng MN và BD bằng
A. 60 °
B. 90 °
C. 45 °
D. 75 °
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 120 ° , SA vuông góc với (ABCD). Gọi M, I lần lượt là trung điểm của BC và SB, góc giữa SM và (ABCD) bằng 60°. Khi đó thể tích của khối chóp I.ABCD bằng