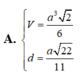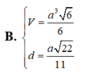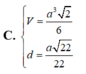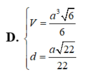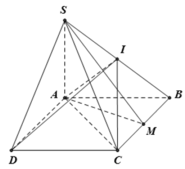
* Ta có SA ⊥ (ABCD) nên AM là hình chiếu của SM trên mặt phẳng (ABCD)
![]()
* ΔABCcó AB = BC = a ( vì ABCD là hình thoi) và ![]() nên ΔABC đều.
nên ΔABC đều.
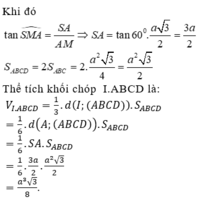

* Ta có SA ⊥ (ABCD) nên AM là hình chiếu của SM trên mặt phẳng (ABCD)
![]()
* ΔABCcó AB = BC = a ( vì ABCD là hình thoi) và ![]() nên ΔABC đều.
nên ΔABC đều.
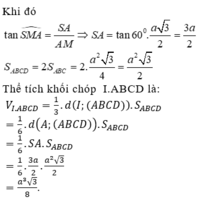
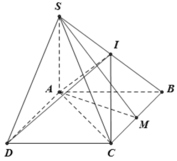
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, BAD = 120°, SA vuông góc với (ABCD). Gọi M, I lần lượt là trung điểm của BC và SB, góc giữa SM và (ABCD) bằng 60°. Khi đó thể tích của khối chóp I.ABCD bằng
A. a 3 6 4
B. a 3 3 8
C. a 3 3 2
D. a 3 3 6
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Biết SA vuông góc với mặt đáy, SB = 2a. Gọi M, N lần lượt là trung điểm SB, BC. Tính thể tích V của khối chóp A.SCNM?
A. V = a 3 3 16
B. C
C. V = a 3 3 24
D. V = a 3 3 8
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, với SA = a 2 , SB = a 3 2 và B A D ⏜ = 60 ∘ và mặt phẳng (SAB) vuông góc với mặt phẳng đáy. Gọi H, K lần lượt là trung điểm của AB, BC. Tính thể tích V của tứ diện K.SDC
A. a 3 4
A. a 3 16
C. a 3 8
D. a 3 12
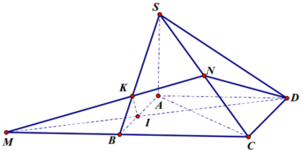
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 ° và SA vuông góc với mặt phẳng (ABCD). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng 45 ° . Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V 1 , khối đa diện còn lại có thể tích V 2 (tham khảo hình vẽ bên).
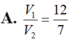
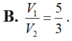
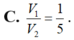
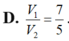
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a với SA = a 2 , SB = a 3 2 , B A D ^ = 60 ∘ và mặt phẳng (SAB) vuông góc với mặt phẳng đáy. Gọi H, K lần lượt là trung điểm của AB, BC. Thể tích tứ diện K.SDC có giá trị là:

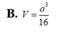
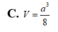
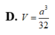
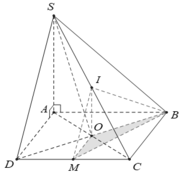
Cho hình chóp S.ABCD có cạnh đáy ABCD là hình vuông tâm O cạnh bằng a, SA vuông góc với (ABCD) và SA = 2a. Gọi I là trung điểm của SC và M là trung điểm của DC. Tính thể tích của khối chóp I.OBM.
A. a 3 24
B. 3 a 3 24
C. a 3 3 24
D. a 3 2 24
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, SA vuông góc với (ABCD) và SA = 2a. Gọi I là trung điểm của SC và M là trung điểm của DC. Tính thể tích của khối chóp I.OBM.
A. V = a 3 24
B. V = 3 a 3 24
C. V = a 3 3 24
D. V = a 3 2 24
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 ° và SA vuông góc với mặt phẳng (ABCD). Góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 450. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2 (tham khảo hình vẽ bên). Tính tỉ số V 1 V 2
A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B; AB = BC = a, AD = 2a, SA ⊥ (ABCD). Góc giữa mặt phẳng (SCD) và (ABCD) bằng 45 ∘ . Gọi M là trung điểm AD. Tính theo a thể tích V khối chóp S.MCD và khoảng cách d giữa hai đường thẳng SM và BD