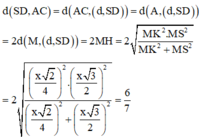Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Biết rằng diện tích mặt cầu ngoại tiếp khối chóp S.ABCD là 4 π dm 2 Khoảng cách giữa hai đường thẳng SD và AC gần nhất với giá trị nào sau đây?
A. 2 7 d m
B. 3 7 d m
C. 4 7 d m
D. 6 7 d m
Chọn D.
Phương pháp: Xác định cạnh của đáy trước.
Cách giải: Bán kính mặt cầu ngoại tiếp khối chóp là ![]()
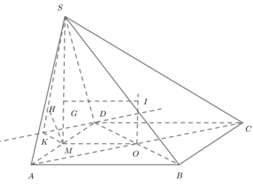
Gọi O là tâm của đáy, I là tâm mặt cầu, G là tâm tam giác SAD, M là trung điểm AD.
Dễ thấy I nằm đồn thời trên trục của tam giác SAD và trục của đáy.
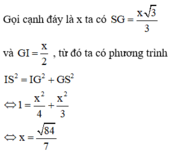
Qua D dựng đường thẳng d song song với AC. Gọi K là hình chiếu cửa M trên d, H là hình chiếu của M trên SD. Suy ra M H ⊥ d , S D .
Ta có: