Ta có: DB\(\perp\)AC(ABCD là hình vuông)
DB\(\perp\)SA(SA\(\perp\)(ABCD))
AC,SA cùng thuộc mp(SAC)
Do đó: DB\(\perp\)(SAC)
=>DB\(\perp\)SC
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Câu3: cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh. Cạnh bên SA vuông góc với đáy.
a/ chứng minh BD vuông (SAC)
b/ chứng minh BD vuông SC
Cho hình chóp S.ABCD có đáy ABCD là hình vuông biết SA
⊥
(ABCD), SCa và SC hợp với đáy một góc
60
o
. Thể tích khối chóp S.ABCD bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông biết SA ⊥ (ABCD), SC=a và SC hợp với đáy một góc 60 o . Thể tích khối chóp S.ABCD bằng
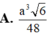
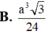
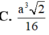
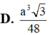
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, S A = a 2 . Tính góc giữa SC và mp (SAB).
cần giải gấp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a với SA vuông góc (ABCD). Kẻ AH vuông góc SB, AK vuông góc SD.
a) chứng minh CD vuông góc (SAD).
b) Chứng minh AK vuông góc SC
c) Gọi M là giao điểm của SC với (AHK). Chứng minh HK vuông góc AM
d)AK=?, AM=? Biết SA = a\(\sqrt{3}\)
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) là
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) là
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) là
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy. Góc giữa đường thẳng SC và mặt phẳng (ABCD) là
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy (ABCD), SC
a
5
. Tính thể tích khối chóp.
A
.
V
a
3
3
3
B
.
V
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy (ABCD), SC = a 5 . Tính thể tích khối chóp.
A . V = a 3 3 3
B . V = a 3 3 6
C . V = a 3 3
D . V = a 3 3 9
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, S A = a 2 . Chứng minh rằng các mặt bên hình chóp là những tam giác vuông.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, S A = a 2 . Chứng minh rằng: (SAC) ⊥ (SBD).
cho hình chóp S.ABCD, đáy là hình vuông,cạnh a. tâm giác SAB và tam giác SAC vuông tại A. góc giữa SC và(ABCD) bằng 30 độ.
a) chứng minh SA vuông góc với (ABCD)
b)cho AH là đường cao tâm giác SAB, chứng minh AH vuông góc với SC
c)góc giữa SC và (SAB)