Question

Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh a và SA vuông góc đáy ABCD và mặt bên (SCD) hợp với đáy một góc 60 ° , M là trung điểm của BC. Tính thể tích hình chóp S.ABMD 

A. a 3 3 4

B.  a 3 3 6

C.  a 3 3 3

D.  a 3 3

Answer 1

Đáp án A

Phương pháp:

Chứng minh góc giữa hai mặt phẳng (SCD) và (ABCD) là SDA bằng cách sử dụng định nghĩa góc giữa hai mặt phẳng là góc giữa hai đường thẳng cùng vuông góc với giao tuyến.

Công thức tính thể tích khối chóp:  V = 1 3 S . h

Cách giải:

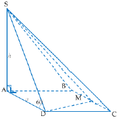
Ta có:  S A ⊥ A B C D ⇒ S A ⊥ C D

Mà A D ⊥ C D ⇒ C D ⊥ S A D ⇒ C D ⊥ S D .

Vì S C D ∩ A B C D = C D A D ⊥ C D S D ⊥ C D nên góc giữa (SCD) và (ABCD) là  S D A = 60 °

Ta có:  h = a . tan 60 ° = a 3

S A B M D = S A B C D − S Δ D C M = a 2 − 1 2 a . a 2 = 3 a 2 4

⇒ V S . A B M D = 1 3 S A B M D . h = 1 3 . 3 a 2 4 . a 3 = a 3 3 4

Chú ý khi giải:

HS thường xác định sai góc giữa hai mặt phẳng dẫn đến đáp số sai.