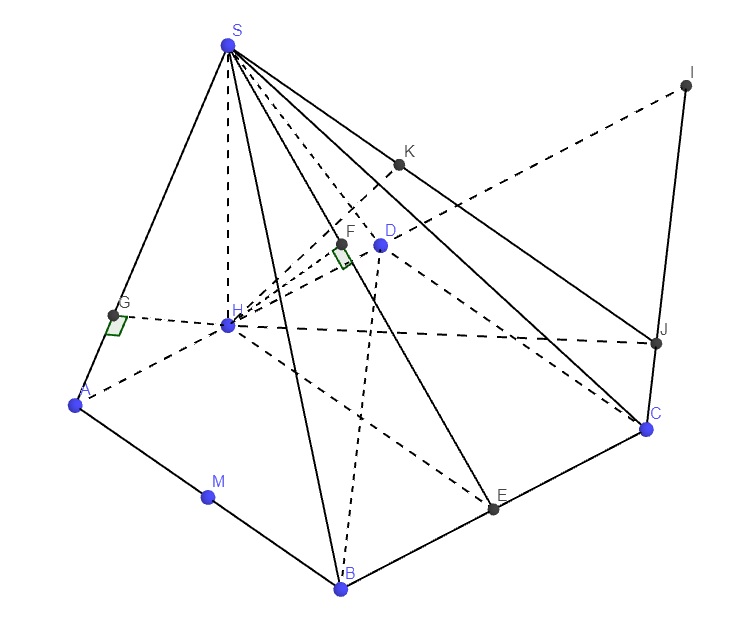
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, tam giác SAD đều và nằm trong mặt phẳng vuông góc với mp(ABCD). Gọi H, M lần lượt là trung điểm của các cạnh AD và AB
a) Tính độ dài đường cao của hình chóp S.ABCD
b) Chứng minh rằng: (SMD) ⊥ (SHC), (SHB) ⊥ (SMD)
c) Tính d(D, (SBC)); d(CD, (SAB)); d(SC, BD))
a.
Do tam giác SAD đều \(\Rightarrow SH\perp AD\)
Mà \(\left\{{}\begin{matrix}\left(SAD\right)\perp\left(ABCD\right)\\AD=\left(SAD\right)\cap\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SH\perp\left(ABCD\right)\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
b.
\(\overrightarrow{MD}.\overrightarrow{HC}=\left(\overrightarrow{MA}+\overrightarrow{AD}\right).\left(\overrightarrow{HD}+\overrightarrow{DC}\right)=\overrightarrow{MA}.\overrightarrow{HD}+\overrightarrow{AD}.\overrightarrow{DC}+\overrightarrow{MA}.\overrightarrow{DC}+\overrightarrow{AD}.\overrightarrow{HD}\)
\(=\overrightarrow{MA}.\overrightarrow{DC}+\overrightarrow{AD}.\overrightarrow{HD}\) (do MA vuông góc HD, AD vuông góc DC nên tích vô hướng =0)
\(=-\dfrac{a}{2}.a+a.\dfrac{a}{2}=0\)
\(\Rightarrow MD\perp HC\)
Lại có \(SH\perp\left(ABCD\right)\Rightarrow SH\perp MD\)
\(\Rightarrow MD\perp\left(SHC\right)\)
Mà \(MD\in\left(SMD\right)\Rightarrow\left(SMD\right)\perp\left(SHC\right)\)
Câu tiếp theo đề sai, 2 mp (SHB) và (SMD) ko vuông góc nhau
(Bởi vì nếu \(\left(SHB\right)\perp\left(SMD\right)\), đồng thời \(\left(SHC\right)\perp\left(SMD\right)\) thì giao tuyến của (SHB) và (SHD) là SH sẽ vuông góc (SMD), điều này hoàn toàn vô lý, nó sẽ dẫn tới 2 mp (SMD) và (ABCD) song song)
c.
Gọi E là trung điểm BC \(\Rightarrow HE\perp BC\)
Trong mp (SHE), từ H kẻ \(HF\perp SE\)
Do \(SH\perp\left(ABCD\right)\Rightarrow SH\perp BC\)
\(\Rightarrow BC\perp\left(SHE\right)\) \(\Rightarrow BC\perp HF\)
\(\Rightarrow HF\perp\left(SBC\right)\Rightarrow HF=d\left(H;\left(SBC\right)\right)\)
Lại có \(DH||BC\Rightarrow d\left(D;\left(SBC\right)\right)=d\left(H;\left(SBC\right)\right)=HF\)
\(HE=AB=a\Rightarrow HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{21}}{7}\)
\(d\left(CD;\left(SAB\right)\right)=d\left(D;\left(SAB\right)\right)\)
\(\left\{{}\begin{matrix}DH\cap\left(SAB\right)=A\\DA=2HA\end{matrix}\right.\) \(\Rightarrow d\left(D;\left(SAB\right)\right)=2d\left(H;\left(SAB\right)\right)\)
Từ H kẻ \(HG\perp SA\)
\(\left\{{}\begin{matrix}SH\perp\left(ABCD\right)\Rightarrow SH\perp AB\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
\(\Rightarrow AB\perp HG\Rightarrow HG\perp\left(SAB\right)\)
\(\Rightarrow HG=d\left(H;\left(SAB\right)\right)\)
Hệ thức lượng: \(HG=\dfrac{SH.HA}{\sqrt{SH^2+HA^2}}=\dfrac{a\sqrt{3}}{4}\)
\(\Rightarrow d\left(CD;\left(SAB\right)\right)=2HG=\dfrac{a\sqrt{3}}{2}\)
Qua C kẻ đường thẳng song song BD cắt AD kéo dài tại I
\(\Rightarrow d\left(SC;BD\right)=d\left(BD;\left(SCI\right)\right)=d\left(D;\left(SCI\right)\right)\)
\(BCID\) là hình bình hành (2 cặp canh đối song song) \(\Rightarrow\left\{{}\begin{matrix}DI=BC=a\\\widehat{DIC}=\widehat{DBC}=45^0\end{matrix}\right.\)
\(\left\{{}\begin{matrix}HD\cap\left(SCI\right)=I\\HI=\dfrac{1}{2}DI+DI=\dfrac{3}{2}DI\end{matrix}\right.\) \(\Rightarrow d\left(H;\left(SCI\right)\right)=\dfrac{3}{2}d\left(D;\left(SCI\right)\right)\)
Kẻ \(HJ\perp CI\), kẻ \(HK\perp SJ\)
\(\Rightarrow HK\perp\left(SCI\right)\Rightarrow HK=d\left(H;\left(SCI\right)\right)\)
\(HJ=SI.sin\widehat{DIC}=\dfrac{3a}{2}.sin45^0=\dfrac{3a\sqrt{2}}{4}\)
Hệ thức lượng: \(HK=\dfrac{SH.HJ}{\sqrt{SH^2+HJ^2}}=\dfrac{3a\sqrt{5}}{10}\)
\(\Rightarrow d\left(SC;BD\right)=\dfrac{2}{3}HK=\dfrac{a\sqrt{5}}{5}\)