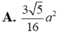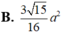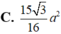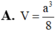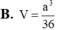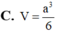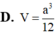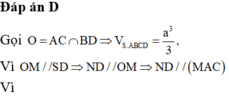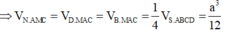Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAa và SA vuông góc với đáy. Gọi M là trung điểm SB, N là điểm thuộc cạnh SD sao cho SN2ND. Tính tỉ số thể tích
V
A
C
M
N
V
S
A
B
C
D
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=a và SA vuông góc với đáy. Gọi M là trung điểm SB, N là điểm thuộc cạnh SD sao cho SN=2ND. Tính tỉ số thể tích V A C M N V S A B C D
![]()
![]()
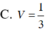
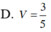
Cho hình chóp S.abcd,có đáy ABCD là hình bình hành. Lấy M là trung điểm của SA, N thuộc SD sao cho SN=2SD a)tìm giao điểm của MN và (ABCD) b) tìm giao điểm của CM và (SBD)
Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, các điểm M, N, P, Q lần lượt là trung điểm của các cạnh SA, SB, SC, SD. Gọi
V
1
,
V
2
lần lượt là thể tích của S.ABC và O.MNPQ. Tính tỉ số
V
1
V
2
. A.
V...
Đọc tiếp
Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, các điểm M, N, P, Q lần lượt là trung điểm của các cạnh SA, SB, SC, SD. Gọi V 1 , V 2 lần lượt là thể tích của S.ABC và O.MNPQ. Tính tỉ số V 1 V 2 .
A. V 1 V 2 = 1
B. V 1 V 2 = 2
C. V 1 V 2 = 4
D. V 1 V 2 = 8
cho hình chóp S.ABCD có đáy hình vuông cạnh a, SA = a, SA ⊥ (ABCD). Gọi H, K lần lượt là trung điểm của cạnh SB,SD; O là tâm hình vuông ABCD.
1/ Chứng minh: (SAB) ⊥ (SBC)
2/ Chứng minh: SC ⊥ (AHK)
cho hình chóp sabcd có đáy abcd là hình vuông cạnh a sa vuông góc với đáy sa=a . gọi M,N lần lượt là trung điểm của SB và SD . Tính số đo góc giữa hai mặt phẳng (AMN) và (ABCD)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm 0; cạnh bên SA vuông góc với mặt phẳng (ABCD) và SA=a. Gọi M,N lần lượt là trung điểm của SD và BC. Tính khoảng cách từ điểm M đến mặt phẳng (SBC)
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm SA,N là điểm thuộc cạnh SB sao cho SN=2NB.
a)Tìm giao điểm P của MN với mặt phẳng (ABCD)
b) Chứng minh PC // (SBD)
c) Gọi H là giao điểm cảu (NPC) với SD và G là trọng tâm của tam giác SCD. Chứng minh (NHG) // (ABCD)
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên tạo với đáy một góc
60
0
. Gọi M là trung điểm của SC. Mặt phẳng đi qua AM và song song với BD cắt SB tại E và cắt SD tại F. Tính thể tích V khối chóp S.AEMF
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên tạo với đáy một góc 60 0 . Gọi M là trung điểm của SC. Mặt phẳng đi qua AM và song song với BD cắt SB tại E và cắt SD tại F. Tính thể tích V khối chóp S.AEMF
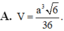
![]()
![]()
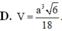
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Cạnh bên SA vuông góc với đáy,SA
2
a
3
Gọi I là trung điểm của mặt phẳng (P) đi qua I và vuông góc với SD. Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P).
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Cạnh bên SA vuông góc với đáy,SA= 2 a 3 Gọi I là trung điểm của mặt phẳng (P) đi qua I và vuông góc với SD. Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P).