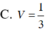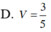E, F lần lượt là trung điểm của SB và SD
=> EF là đường trung bình tam giác SBD => EF // BD => (SD,EF) = (SD,BD) = SDB
BD là đường chéo hình thoi cạnh a => BD = a√2
SB=SD=\(\sqrt{\left(a\sqrt{3}\right)^2+a^2}=2a\) (tam giác vuông)
Gọi H là trung điểm BD thì cosSDB=DH/SD=√2/4 => SDB=arccos\(\dfrac{\sqrt{2}}{4}\approx69^o\)