Các câu hỏi tương tự
Cho hình chóp
S
.
A
B
C
D
có đáy là hình thang vuông tại A và B. Biết
A
D
2
a
,
A
B
B
C
S
A
a
. Cạnh bên SA vuông góc với mặt phẳng đáy, gọi M là trung điểm cạnh AD. Tính khoảng cách h từ M đến mặt phẳng (SCD). A.
h
a
3...
Đọc tiếp
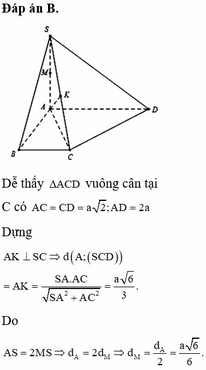
Cho hình chóp S . A B C D có đáy là hình thang vuông tại A và B. Biết A D = 2 a , A B = B C = S A = a . Cạnh bên SA vuông góc với mặt phẳng đáy, gọi M là trung điểm cạnh AD. Tính khoảng cách h từ M đến mặt phẳng (SCD).
A. h = a 3 .
B. h = a 6 3 .
C. h = a 6 6 .
D. h = a 3 6
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B và AD 2a, AB BC SA a. Cạnh bên SA vuông góc với đáy, với M là trung điểm AD. Tính khoảng cách h từ M đến mặt phẳng (SCD). A.
h
a
3
B.
h
a
6
6
C.
h
a
6
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B và AD = 2a, AB = BC = SA = a. Cạnh bên SA vuông góc với đáy, với M là trung điểm AD. Tính khoảng cách h từ M đến mặt phẳng (SCD).
A. h = a 3
B. h = a 6 6
C. h = a 6 3
D. h = a 3 6
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên
S
C
a
15
.
Tam giác SAD là tam giác đều cạnh bằng 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm AD, khoảng cách từ B đến mặt phẳng (SHC) bằng
2
a
6
.
Tính thể tích V của khối chóp S.ABCD? A.
V
8
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên S C = a 15 . Tam giác SAD là tam giác đều cạnh bằng 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm AD, khoảng cách từ B đến mặt phẳng (SHC) bằng 2 a 6 . Tính thể tích V của khối chóp S.ABCD?
A. V = 8 a 3 6 .
B. V = 12 a 3 6 .
C. V = 4 a 3 6 .
D. V = 24 a 3 6 .
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại C và D,
A
B
C
^
30
o
. Biết ACa,
C
D
a
2
và
S
A
a
3
2
cạnh SA vuông góc với mặt phẳng đáy. Khoảng cách từ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại C và D, A B C ^ = 30 o . Biết AC=a, C D = a 2 và S A = a 3 2 cạnh SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng (SCD) bằng
A. a 6
B. a 6 2
C. a 6 4
D. a 3 2
Cho hình chóp S.ABCDvới đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên
S
C
a
15
.
Tam giác SAD là tam giác đều cạnh 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm của cạnh AD, khoảng cách từ B tới mặt phẳng (SHC) bằng
2
6
a
.
Tính thể tích V của khối chóp S,ABCD? A.
V
8...
Đọc tiếp
Cho hình chóp S.ABCDvới đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên S C = a 15 . Tam giác SAD là tam giác đều cạnh 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm của cạnh AD, khoảng cách từ B tới mặt phẳng (SHC) bằng 2 6 a . Tính thể tích V của khối chóp S,ABCD?
A. V = 8 6 a 3
B. V = 12 6 a 3
C. V = 4 6 a 3
D. V = 24 6 a 3
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD). Tứ giác ABCD là hình vuông cạnh a,
S
A
2
a
. Gọi H là hình chiếu vuông góc của A trên SB. Tính khoảng cách từ H đến mặt phẳng (SCD). A.
4
a
5
5
.
B.
4
a...
Đọc tiếp
Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD). Tứ giác ABCD là hình vuông cạnh a, S A = 2 a . Gọi H là hình chiếu vuông góc của A trên SB. Tính khoảng cách từ H đến mặt phẳng (SCD).
A. 4 a 5 5 .
B. 4 a 5 25 .
C. 2 a 5 5 .
D. 8 a 5 25 .
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Gọi I là trung điểm của AB, hai mặt phẳng (SIC) và (SID) cùng vuông góc với đáy. Biết ADAB2a, BCa, khoảng cách từ I đến (SCD) là
3
a
2
4
. Thể tích khối chóp S.ABCD là
A
.
a
3
B
.
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B. Gọi I là trung điểm của AB, hai mặt phẳng (SIC) và (SID) cùng vuông góc với đáy. Biết AD=AB=2a, BC=a, khoảng cách từ I đến (SCD) là 3 a 2 4 . Thể tích khối chóp S.ABCD là
A . a 3
B . a 3 3
C . 3 a 3
D . a 3 3 2
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B; AB BC a; AD 2a;
S
A
⊥
A
B
C
D
. Góc giữa mặt phẳng ( SCD ) và ( ABCD ) bằng
45
o
. Gọi M là trung điểm AD. Tính theo a thể tích V khối chóp S.MCD và khoảng cách d giữa hai đường thẳng SM và BD A.
V...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B; AB = BC = a; AD = 2a; S A ⊥ A B C D . Góc giữa mặt phẳng ( SCD ) và ( ABCD ) bằng 45 o . Gọi M là trung điểm AD. Tính theo a thể tích V khối chóp S.MCD và khoảng cách d giữa hai đường thẳng SM và BD
A. V = a 3 2 6 d = a 22 11
B. V = a 3 6 6 d = a 22 11
C. V = a 3 2 6 d = a 22 22
D. V = a 3 6 6 d = a 22 22
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên đáy ABCD trùng với trung điểm AB. Biết
A
B
a
,
B
C
2
a
,
B
D
a
10
.
Góc giữa hai mặt phẳng (SBD) và đáy là
60
°
.
Tính d là khoảng cách từ A đến mặt phẳng (SCD) gần với giá trị nào nhất trong các giá trị sau đây...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên đáy ABCD trùng với trung điểm AB. Biết A B = a , B C = 2 a , B D = a 10 . Góc giữa hai mặt phẳng (SBD) và đáy là 60 ° . Tính d là khoảng cách từ A đến mặt phẳng (SCD) gần với giá trị nào nhất trong các giá trị sau đây ?
A. 0,80a
B. 0,85a
C. 0,95a
D. 0,98a