Đáp án D
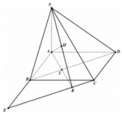
Dựng ![]()
Dựng ![]()
Khi đó Cx cắt AB tại E và AK tại I suy ra BI là đường trung bình của ∆AEK ( Do BD qua trung điểm O của AC)
Ta có: 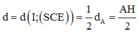
Do 
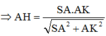
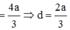
Đáp án D

Dựng ![]()
Dựng ![]()
Khi đó Cx cắt AB tại E và AK tại I suy ra BI là đường trung bình của ∆AEK ( Do BD qua trung điểm O của AC)
Ta có: 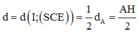
Do 
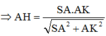
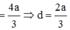
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, BC = 2a. Cạnh bên SA = 2a và SA vuông góc với mặt phẳng đáy. Khoảng cách giữa SC và BD bằng :
A. 2 a 3
B. a 3 2
C. 4 a 3
D. 3 a 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt phẳng đáy. Biết S A = 2 2 a , A B = a , B C = 2 a . Khoảng cách giữa hai đường thẳng BD và SC bằng
A. 2 7 a 7
B. 7 a 7
C. 7 a
D. 6 a 5
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = a , A D = 2 a ; cạnh bên SA vuông góc với mặt đáy và S A = a 5 Khoảng cách giữa hai đường thẳng AB và SD bằng
A. 2 a 5 3
B. a 5
C. a 5 2
D. 2 a
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, cạnh SA vuông góc với mặt phẳng (ABCD) và SA=a. Tính theo a khoảng cách d giữa hai đường thẳng SC và BD.
A. d = a 2 2
B. d = a 3 3
C. d = a 5 5
D. d = a 6 6
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, cạnh SA vuông góc với mặt phẳng (ABCD) và SA=a. Tính theo a khoảng cách d giữa hai đường thẳng SC và BD.
A. d = a 2 2
B. d = a 3 3
C. d = a 5 5
D. d = a 6 6
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với A B = a , B C = a 3 , cạnh S A = 2 a , S A ⊥ A B C D . Gọi α là góc giữa đường thẳng SC với mặt phẳng (ABCD). Giá trị tan bằng
A. 2
B. 2
C. 1
D. 1 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=a và vuông góc với mặt đáy (ABCD). Khoảng cách giữa 2 đường thẳng SC và BD bằng
A. a 3 4
B. a 6 3
C. a 2
D. a 6 6
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy và S A = 2 a . Góc giữa đường thẳng SC và mặt phẳng (ABCD) là α . Khi đó t a n α bằng:
A. 2
B. 2 3
C. 2
D. 2 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = 2a, SA = 2a và SA ⊥ (ABCD). Gọi a là góc giữa 2 đường thẳng SC và BD. Khi đó, cosa bằng
A. - 5 5
B. 0
C. 5 5
D. 1 2