Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy là hình bình hành:
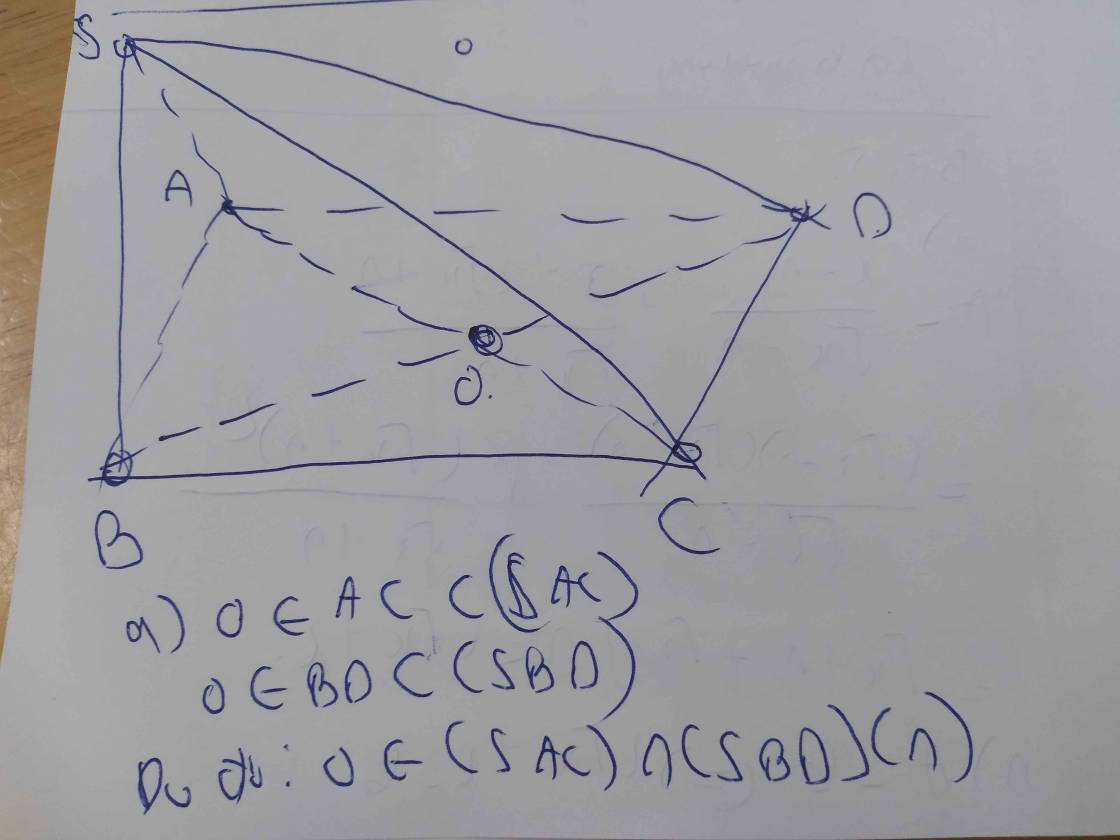
a, Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
b, Gọi M,N lần lượt là các điểm trên các cạnh SB và SC sao cho MS=2MB, NS=NC. Mặt phẳng (AMN) cắt cạnh SD tại K. Chứng minh MK//(ABCD)
Cho hình chóp (S.ABCD) có đáy (ABCD) là hình bình hành; M, N lần lượt là trung điểm của (SB, SD) a) Chứng minh đường thẳng BD song song với mặt phẳng (AMN) b) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD). Tìm giao điểm của đường thẳng MN và mặt phẳng (SAC)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O và M là trung điểm của SD.
a, tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
b, chứng minh rằng MO song song với mặt phẳng (SAD).
Cho hình chóp S.ABCD có đáy ABCD là một hình bình hành tâm O. Gọi M là trung điềm SB và N là điểm trên cạnh SA sao cho SN=2SA.
a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD)
b) Tìm giao điểm H của AD với mặt phẳng (OMN), giao điểm K của BC với mặt phẳng (OMN)
c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (OMN).
cho hình chóp s.abcd có đáy là hình bình hành. Gọi M,N lần lượt là trung điểm của các cạng SA,SC, và G là trọng tâm của △ABC
a) tìm giao tuyến của hai mặt phẳng (SAC) và (SBD)
b) tìm giao điểm BC và mặt phẳng (GMN)
c) xác định thiết diện của hình chóp khi cắt bởi mặt phẳng (GMN)
cho hình chóp S.ABCD, đáy ABCD là hình thang, có đáy lớn AD. Gọi H,K lần lượt là trung điểm SB, SD, I = AC giao BD.
a) tìm giao tuyến của 2 mặt phẳng (SBD) và (SAC)
b) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
c) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
cho hình chóp S.ABCD, đáy ABCD là hình thang, có đáy lớn AB. Gọi M,N lần lượt là trung điểm SA, SC, E = AC giao BD.
a) tìm giao tuyến của 2 mặt phẳng (SAC) và (SBD)
b) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
c) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
cho hình chóp S.ABCD, đáy ABCD là hình thang, có đáy lớn AB. Gọi M,N lần lượt là trung điểm SA, SC, E = AC giao BD.
a) tìm giao tuyến của 2 mặt phẳng (SAC) và (SBD)
b) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
c) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M , K lần lượt là trung điểm của cạnh SC và BC ; N là trọng tâm ABC và F là giao điểm của AN và DC
. a) Tìm giao tuyến của mặt phẳng AMN và SCD .
b) Gọi E là giao điểm của SO và AM , I là giao điểm của SD và AMN . Chứng minh rằng N, E, I thẳng hàng và NI / / SBC
. c) Tính tỉ số diện tích của tam giác FKM và tam giác KAI .
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M , K lần lượt là trung điểm của cạnh SC và BC ; N là trọng tâm ABC và F là giao điểm của AN và DC
. a) Tìm giao tuyến của mặt phẳng AMN và SCD .
b) Gọi E là giao điểm của SO và AM , I là giao điểm của SD và AMN . Chứng minh rằng N, E, I thẳng hàng và NI / / SBC
. c) Tính tỉ số diện tích của tam giác FKM và tam giác KAI .