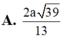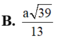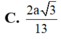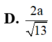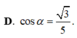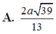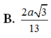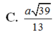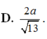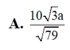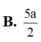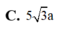Question

Cho hình chóp S.ABC. Điểm M thuộc cạnh SA và SM = 2/3 SA a) Viết hệ thức liên hệ giữa các cặp véc-tơ vec SM và SA, MA và AS . b) Tìm điểm N sao cho vecto MN =- 2/3 vecto BA

Answer 1

a: Ta có: M nằm giữa S và A

=>SM+MA=SA

=>\(MA=SA-SM=SA-\frac23SA=\frac13SA\)

=>\(\overrightarrow{AM}=\frac13\cdot\overrightarrow{AS}\)

=>\(\overrightarrow{MA}=-\frac13\cdot\overrightarrow{AS}\)

Vì \(SM=\frac23SA\)

nên \(\overrightarrow{SM}=\frac23\cdot\overrightarrow{SA}\)

b: \(\overrightarrow{MN}=-\frac23\cdot\overrightarrow{BA}\)

=>\(\overrightarrow{MN}=\frac23\cdot\overrightarrow{AB}\)

=>MN//AB và MN=2/3AB

Xét ΔSMN và ΔSAB có

\(\frac{SM}{SA}=\frac{MN}{AB}\left(=\frac23\right)\)

\(\hat{SMN}=\hat{SAB}\) (hai góc đồng vị, MN//AB)

Do đó: ΔSMN~ΔSAB

=>\(\hat{SNM}=\hat{SBA}\) và SN/SB=MN/AB=2/3

Giả sử N nằm giữa S và B sao cho SN/SB=2/3

Xét ΔSAB có \(\frac{SM}{SA}=\frac{SN}{SB}\left(=\frac23\right)\)

nên MN//AB(đúng với giả thiết)

=>N nằm giữa S và B sao cho \(SN=\frac23SB\)