Đáp án: A.
§ Hướng dẫn giải:
Gọi N là trung điểm của cạnh đáy AC.
Khi đó BC // (SMN)
⇒ d(SM,BC)=d(B,(SMN))=d(A,(SMN))
Gọi H là hình chiếu vuông góc của A trên đoạn SM.
Ta có thể chứng minh được M N ⊥ ( S A M )
từ đó A H ⊥ ( S M N )
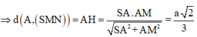
Đáp án: A.
§ Hướng dẫn giải:
Gọi N là trung điểm của cạnh đáy AC.
Khi đó BC // (SMN)
⇒ d(SM,BC)=d(B,(SMN))=d(A,(SMN))
Gọi H là hình chiếu vuông góc của A trên đoạn SM.
Ta có thể chứng minh được M N ⊥ ( S A M )
từ đó A H ⊥ ( S M N )
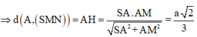
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC=2a, SA vuông góc với mặt phẳng đáy và SA=a 3 . Gọi M là trung điểm của AC. Khoảng cách giữa hai đường thẳng AB và SM bằng:
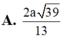
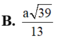
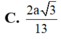
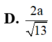
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh bên SA vuông góc với đáy và SA=a, AB=BC=a. Gọi M là điểm thuộc AB sao cho . Tính khoảng cách d từ điểm S đến đường thẳng CM.
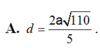
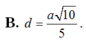
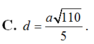
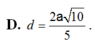
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=3a, BC=4a. Cạnh bên SA vuông góc với đáy. Góc tạo bởi giữa SC với đáy bằng 60 0 . Gọi M là trung điểm AC, tính khoảng cách giữa hai đường thẳng AB và SM
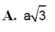
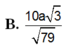
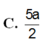
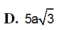
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC=2a, SA vuông góc với mặt phẳng đáy và SA=2a 3 . Gọi M là trung điểm của AC. Khoảng cách giữa hai đường thẳng AB và SM bằng

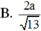

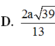
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, BC = a, cạnh bên SA vuông góc với đáy, SA = a 3 . Gọi M là trung điểm của AC. Tính cotang góc giữa hai mặt phẳng (SBM) và (SAB).
A. 3 2
B. 1
C. 21 7
D. 2 7 7
Hình chóp S.ABC có đáy ABC là tam giác vuông tại C. Có CA = a,CB = b cạnh SA = h vuông góc với đáy. Gọi D là trung điểm của cạnh AB. Khoảng cách giữa hai đường thẳng AC và SD là?
A. a h a 2 + h 2 .
B. b h b 2 + 4 h 2 .
C. a h b 2 + 4 h 2 .
D. a h b 2 + 2 h 2 .
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B\),\(BC=a\), cạnh bên \(SA\) vuông góc với đáy ,\(SA=a\sqrt[]{3}\) .Gọi \(M\) là trung điểm của \(AC\).Tính cot góc giữa hai mặt phẳng \(\left(SBM\right)\) và \(\left(SAB\right)\).
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, B C = 2 a , SA vuông góc với mặt phẳng đáy và S A = 2 a 3 . Gọi M là trung điểm của AC. Khoảng cách giữa hai đường thẳng AB và SM bằng
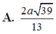
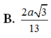
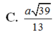
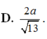
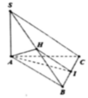
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với đáy. Biết SA = a; AB = a; B C = a 2 . Gọi I là trung điểm của BC. Cosin của góc giữa 2 góc đường thẳng AI và SC là?
A. 2 3
B. - 2 3
C. 2 3
D. 2 8