Đáp án: A.
Hướng dẫn giải: Gọi H là trung điểm của SB
⇒ IH song song với SC.
Do đó SC//(AHI)
![]()
Ta có A I = A B 2 + B I 2 = a 6 2
và I H = S C 2 = S A 2 + A C 2 2 = a
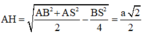
Áp dụng định lý cosin trong tam giác AHI, có
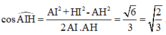
Đáp án: A.
Hướng dẫn giải: Gọi H là trung điểm của SB
⇒ IH song song với SC.
Do đó SC//(AHI)
![]()
Ta có A I = A B 2 + B I 2 = a 6 2
và I H = S C 2 = S A 2 + A C 2 2 = a
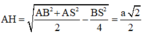
Áp dụng định lý cosin trong tam giác AHI, có
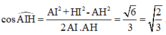
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC=2a, SA vuông góc với mặt phẳng đáy và SA=a 3 . Gọi M là trung điểm của AC. Khoảng cách giữa hai đường thẳng AB và SM bằng:
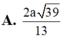
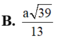
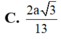
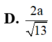
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, BC = 2a, cạnh SA vuông góc với đáy và SA = 2a. Khoảng cách giữa hai đường thẳng AB và SC là
A . a 3
B . 2 a
C . a 2
D . a 5
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BC=2a, SA vuông góc với mặt phẳng đáy và SA=2a 3 . Gọi M là trung điểm của AC. Khoảng cách giữa hai đường thẳng AB và SM bằng

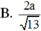

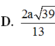
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, BC = a, cạnh bên SA vuông góc với đáy, SA = a 3 . Gọi M là trung điểm của AC. Tính cotang góc giữa hai mặt phẳng (SBM) và (SAB).
A. 3 2
B. 1
C. 21 7
D. 2 7 7
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=3a, BC=4a. Cạnh bên SA vuông góc với đáy. Góc tạo bởi giữa SC với đáy bằng 60 0 . Gọi M là trung điểm AC, tính khoảng cách giữa hai đường thẳng AB và SM
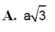
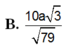
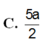
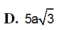
Hình chóp S.ABC có đáy ABC là tam giác vuông tại C. Có CA = a,CB = b cạnh SA = h vuông góc với đáy. Gọi D là trung điểm của cạnh AB. Khoảng cách giữa hai đường thẳng AC và SD là?
A. a h a 2 + h 2 .
B. b h b 2 + 4 h 2 .
C. a h b 2 + 4 h 2 .
D. a h b 2 + 2 h 2 .
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a, cạnh bên SA vuông góc với đáy là S A = a 2 . Gọi M là trung điểm của AB. Khoảng cách giữa SM và BC bằng bao nhiêu?
A. a 2 3
B. a 2
C. a 3 3
D. a 3 2
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt đáy và SA = 2a. Gọi M là trung điểm của SC. Tính côsin của góc α là góc giữa đường thẳng BM và mặt phẳng (ABC).
A. cos α = 7 14
B. cos α = 2 7 7
C. cos α = 5 7
D. cos α = 2 7
Cho hình chóp tam giác S.ABC có SA vuông góc với mặt đáy, tam giác ABC cân tại A. Trên cạnh AB lấy điểm D sao cho AB = 3AD. Gọi H là hình chiếu của B lên CD, M là trung điểm CH. Tính theo a thể tích khối chóp S.ABM biết SA = AM = a và BM = 2/3 a