Question

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Gọi I là trung điểm của AB, hình chiếu của S lên mặt phẳng (ABC) là trung điểm của CI, góc giữa SA và mặt đáy bằng 45 độ. Gọi G là trọng tâm của tam giác SBC. Tính khoảng cách (SA,CG) 

Answer 1

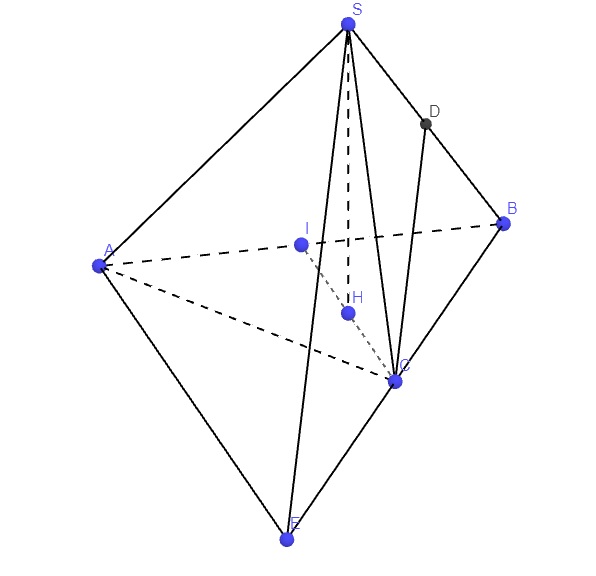
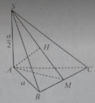
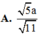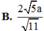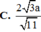Gọi D là trung điểm SB \(\Rightarrow G\) thuộc CD

Lấy E đối xứng B qua C \(\Rightarrow CD\) là đường trung bình tam giác SBE \(\Rightarrow CD||\left(SAE\right)\)

Gọi H là trung điểm CI \(\Rightarrow SH\perp\left(ABC\right)\)

\(d\left(SA;CG\right)=d\left(CD;\left(SAE\right)\right)=d\left(C;\left(SAE\right)\right)\)

\(CI||AE\) (đường trung bình) mà H thuộc CI \(\Rightarrow d\left(C;\left(SAE\right)\right)=d\left(H;\left(SAE\right)\right)\)

Từ H kẻ HF vuông góc SA, từ H kẻ HK vuông góc SF

HK là đoạn cần tính

AIHF là hình chữ nhật nên \(HF=AI=\dfrac{a}{2}\)

Tính SH => HK

Answer 2