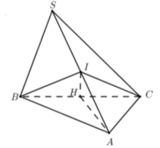
Gọi I là trung điểm của SA.
Tam giác SAB, SAC vuông tại B , C ⇒ I S = I A = I B = I C ⇒ I là tâm mặt cầu ngoại tiếp chóp S.ABC.
Gọi H là trung điểm của BC. Vì vuông tại là tâm đường tròn ngoại tiếp tam giác ABC.
⇒ I H ⊥ A B C .
Gọi R là bán kính mặt cầu ngoại tiếp chóp S.ABC. Theo bài ra ta có:

Xét tam giác vuông ABC có:
B C = A B 2 + A C 2 = 2 ⇒ A H = 1
Xét tam giác vuông IAH có:
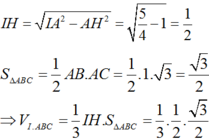
Ta có:
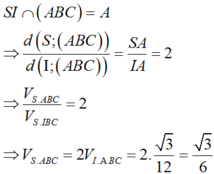
Xét tam giác vuông SAB có
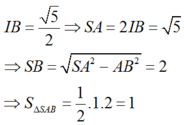
Ta có
Chọn A.



