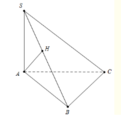
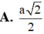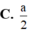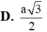Vì \(SB\) là đường cao của tam giác \(SBC\), và ta đã biết \(SB = a \sqrt{3}\), nên ta có thể sử dụng định lý Pythagoras trong tam giác \(SBC\) để tính độ dài \(SC\):
\[SC^2 = SB^2 - BC^2.\]
Với \(SB = a \sqrt{3}\) và \(BC = \frac{a}{\sqrt{2}}\) (vì tam giác \(ABC\) là tam giác vuông cân), ta có:
\[SC^2 = (a \sqrt{3})^2 - \left(\frac{a}{\sqrt{2}}\right)^2 = 3a^2 - \frac{a^2}{2} = \frac{6a^2 - a^2}{2} = \frac{5a^2}{2}.\]
Vậy, \(SC = \sqrt{\frac{5a^2}{2}} = \frac{a \sqrt{10}}{2}.\)
Do đó, khoảng cách từ điểm \(C\) đến mặt phẳng \((SAB)\) là \(\frac{a \sqrt{10}}{2}\).