Cho hình chóp S. ABCD. Gọi A 1 là trung điểm của cạnh SA và A 2 là trung điểm của đoạn A A 1 . Gọi (α) và (β) là hai mặt phẳng song song với mặt phẳng (ABCD) và lần lượt đi qua A 1 , A 2 . Mặt phẳng (α) cắt các cạnh SB, SC, SD lần lượt tại B 1 , C 1 , D 1 . Mặt phẳng (β) cắt các cạnh SB, SC, SD lần lượt tại B 2 , C 2 , D 2 . Chứng minh:
a) B 1 , C 1 , D 1 lần lượt là trung điểm của các cạnh SB, SC, SD.
b) B 1 B 2 = B 2 B , C 1 C 2 = C 2 C , D 1 D 2 = D 2 D .
c) Chỉ ra các hình chóp cụt có một đáy là tứ giác ABCD.
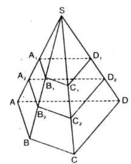
a) Chứng minh B 1 , C 1 , D 1 lần lượt là trung điểm của các cạnh SB, SC, SD
Ta có:
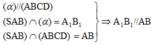
⇒ A 1 B 1 là đường trung bình của tam giác SAB.
⇒ B 1 là trung điểm của SB (đpcm)
*Chứng minh tương tự ta cũng được:
• C 1 là trung điểm của SC.
• D 1 là trung điểm của SD.
b) Chứng minh B 1 B 2 = B 2 B , C 1 C 2 = C 2 C , D 1 D 2 = D 2 D .
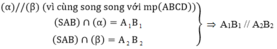
⇒ A 2 B 2 là đường trung bình của hình thang A 1 B 1 B A
⇒ B 2 là trung điểm của B 1 B
⇒ B 1 B 2 = B 2 B (đpcm)
*Chứng minh tương tự ta cũng được:
• C 2 là trung điểm của C 1 C 2 ⇒ C 1 C 2 = C 2 C
• D 2 là trung điểm của D 1 D 2 ⇒ D 1 D 2 = D 2 D .
c) Các hình chóp cụt có một đáy là tứ giác ABCD, đó là : A 1 B 1 C 1 D 1 . A B C D v à A 2 B 2 C 2 D 2 . A B C D