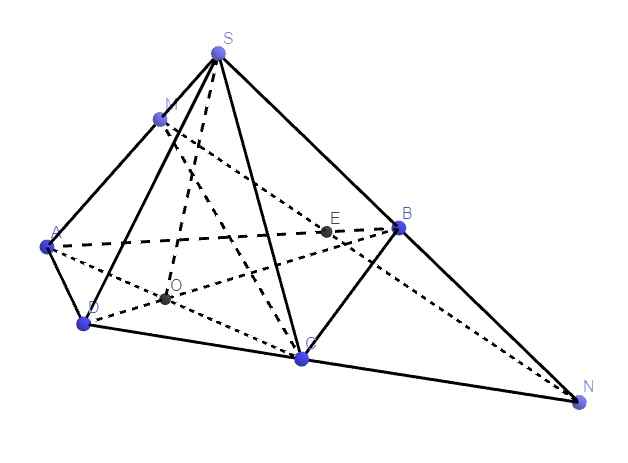
Gọi O là giao điểm AC và BD
\(\left\{{}\begin{matrix}O\in AC\in\left(SAC\right)\\O\in BD\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow O=\left(SAC\right)\cap\left(SBD\right)\)
\(\left\{{}\begin{matrix}S\in\left(SAC\right)\\S\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow S=\left(SAC\right)\cap\left(SBD\right)\)
\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
b. Trong mp ((SAB), nối MN cắt AB tại E
\(\left\{{}\begin{matrix}E\in MN\in\left(CMN\right)\\E\in AB\in\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow E\in\left(CMN\right)\cap\left(ABCD\right)\)
\(\left\{{}\begin{matrix}C\in\left(CMN\right)\\C\in\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow C\in\left(CMN\right)\cap\left(ABCD\right)\)
\(\Rightarrow CE=\left(CMN\right)\cap\left(ABCD\right)\)