Đáp án D
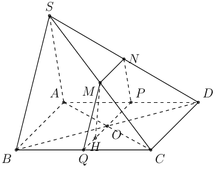
Qua O dựng đường thẳng P Q ∥ A B . Vậy P, Q lần lượt là trung điểm của AD và BC.
Qua P dựng đường thẳng P N ∥ S A . Vậy N là trung điểm của SD
Qua Q dựng đường thẳng Q M ∥ S B . Vậy M là trung điểm của SC.
Nối M và N ⇒ thiết diện của (P) và hình chóp S.ABCD là tứ giác MNPQ.
Vì P Q ∥ C D , M N ∥ C D ⇒ P Q ∥ M N . Vậy tứ giác MNPQ là hình thang.
Ta có P Q = A B = 8 $ , M N = 1 2 A B = 4, M Q = N P = 1 2 S A = 3 . Vậy MNPQ là hình thang cân.
Gọi H là chân đường cao hạ từ đỉnh M của hình thang MNPQ. Khi đó ta có
H Q = 1 4 P Q = 2 ⇒ M H = M Q 2 − H Q 2 = 5
Vậy diện tích của thiết diện cần tìm là S = ( M N + P Q ) M H 2 = 6 5 .



