Do SABCD là chóp tứ giác đều \(\Rightarrow BD\perp\left(SAC\right)\)
Mà \(M\in AC\Rightarrow M\in\left(SAC\right)\)
\(\Rightarrow BD\perp SM\)
Hay góc giữa hai đường thẳng đã cho là 90 độ
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M là điểm trên đoạn SD sao cho SM=2MD.
Tan góc giữa đường thẳng BM và mặt phẳng (ABCD) là
A. 1 3
B. 5 5
C. 3 3
D. 1 5
1.Cho hình lập phương ABCD.EFGH. Hãy tính góc giữa 2 vecto AF và vecto EG
2.Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc (IJ,CD) bằng?
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi M là trung điểm của SD (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng BM và AD bằng
A. 3 5 10
B. 3 5 20
C. 55 10
D. 155 20
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a, gọi φ là góc giữa hai mặt phẳng (SAB) và (CSD) Tính cos φ
A. cos φ = 1 2
B. cos φ = 1 6
C. cos φ = 1 3
D. cos φ = 1 4
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M là trung điểm của SD (tham khảo hình vẽ bên). Tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng
A. 2 2
B. 3 2
C. 2 3
D. 1 3
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M là trung điểm của SD (tham khảo hình vẽ bên). Tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng:
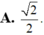
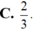
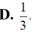
Cho hình chóp tứ giác đều có tất cả các cạnh bằng d. Gọi M là trung điểm của SD. O là giao điểm của hai đường chéo AC và BD. Tang của góc tạo bởi hai đường thẳng BM và SO là:
A . 2 2
B . 3
C . 2 3
D . 3
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Côsin góc giữa hai mặt phẳng (SAB) và (SAD) bằng
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm của CD góc giữa SM và mặt phẳng đáy bằng 60 o Độ dài cạnh SA bằng
A. a 3
B. a 15
C. a 3 2
D. a 15 2
