(Tự vẽ hình)
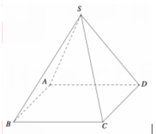
Do hình chóp \(S.ABC\) là hình chóp đều
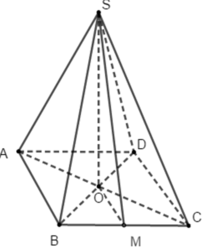
\(\Rightarrow ABC\) là tam giác đều cạnh \(a\) và \(SO\perp\left(ABC\right)\) với \(O\) là tâm ngoại tiếp tam giác \(ABC\)
Gọi \(AH\perp BC\) thì \(H\) là trung điểm \(BC\)
Ta có: \(AH=\sqrt{AB^2-BH^2}=\sqrt{a^2-\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow AO=\dfrac{2}{3}AH=\dfrac{a\sqrt{3}}{3}\); \(OH=\dfrac{1}{2}AH=\dfrac{a\sqrt{3}}{6}\)
Ta có: \(\left(SA;\left(ABC\right)\right)=\left(SA,AO\right)=\widehat{SAO}\)
Tam giác \(SAO\) vuông tại \(O\Rightarrow cos\widehat{SAO}=\dfrac{AO}{SA}=\dfrac{\sqrt{3}}{3}\Rightarrow\widehat{SAO}\approx55^0\)
Lại có: \(\Delta SBC\) đều \(\Rightarrow SH=\dfrac{a\sqrt{3}}{2}\)
Ta có: \(\left(\left(SBC\right),\left(ABC\right)\right)=\widehat{SHO}\)
\(cos\widehat{SHO}=\dfrac{OH}{SH}=\dfrac{1}{3}\Rightarrow\widehat{SHO}\approx70,5^0\)