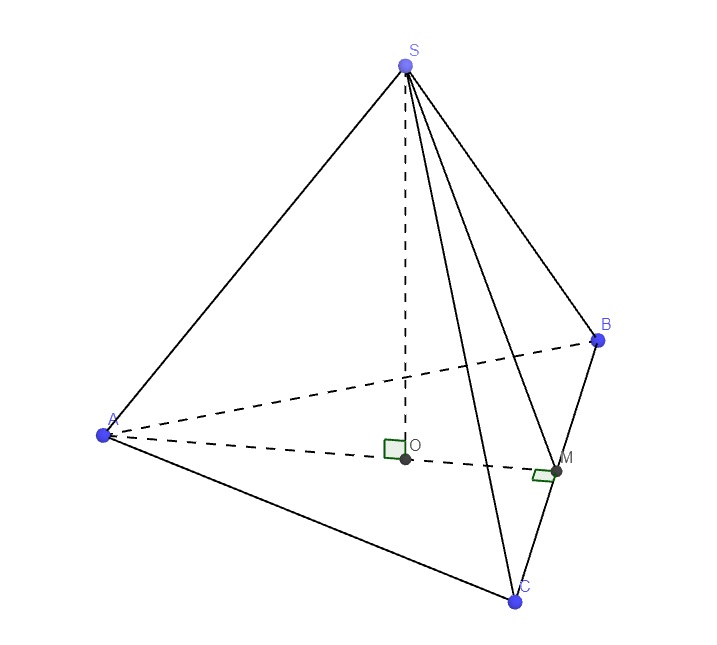
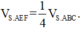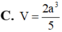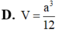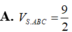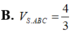ABC đều và M là trung điểm BC \(\Rightarrow AM\perp BC\)
Chóp S.ABC đều và O là tâm đáy \(\Rightarrow SO\perp\left(ABC\right)\Rightarrow SO\perp OM\) hay tam giác SOM vuông tại O
Chóp S.ABC đều \(\Rightarrow SB=SC\) hay tam giác SBC cân tại S \(\Rightarrow SM\perp BC\)
\(SA=SB=SC=3a\)
a.
\(AM=\sqrt{AB^2-BM^2}=\sqrt{AB^2-\left(\dfrac{BC}{2}\right)^2}=\sqrt{\left(2a\right)^2-a^2}=a\sqrt{3}\)
b.
\(S_{\Delta ABC}=\dfrac{1}{2}AM.BC=a^2\sqrt{3}\)
c.
\(MB=\dfrac{1}{2}BC=a\)
\(SM=\sqrt{SB^2-BM^2}=\sqrt{\left(3a\right)^2-a^2}=2a\sqrt{2}\)
d.
\(S_{\Delta SBC}=\dfrac{1}{2}SM.BC=2a^2\sqrt{2}\)
e.
Theo tính chất trọng tâm: \(OM=\dfrac{1}{3}AM=\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow SO=\sqrt{SM^2-OM^2}=\dfrac{a\sqrt{69}}{3}\)