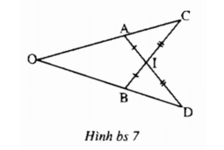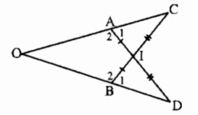
+) Xét ∆AIC và ∆BID có:
AI = BI (giả thiết)
∠AIC = ∠BID ( hai góc đối đỉnh).
IC = ID ( giả thiết)
Suy ra: ∆AIC = ∆BID (c.g.c)
Suy ra: ∠C = ∠D; ∠A1 = ∠B1 (1)
+) Lại có: ∠A1 + ∠A2 = 180º (hai góc kề bù)
Và ∠B1 + ∠B2 = 180º (hai góc kề bù)
Suy ra: ∠A2 = ∠B2
+) Xét tam giác OAD và ∆ OBC có:
∠A2 = ∠B2 (chứng minh trên)
AD = BC (vì AI + ID = BI + IC)
∠D = ∠C (chứng minh trên)
Suy ra: ∆OAD = ∆ OBC (g.c.g)
Suy ra: OA = OB (hai cạnh tương ứng).