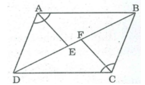
Ta có:
△ ABE = △ CDF (g.c.g) ⇒ S A B E = S C D F (l)
△ AED = △ CFB (g.c.g) ⇒ S A E D = S C F B (2)
Từ (1) và (2) ⇒ S A B E + S C F B = S C D F + S A E D
Hay S A B C F E = S A D C F E

Ta có:
△ ABE = △ CDF (g.c.g) ⇒ S A B E = S C D F (l)
△ AED = △ CFB (g.c.g) ⇒ S A E D = S C F B (2)
Từ (1) và (2) ⇒ S A B E + S C F B = S C D F + S A E D
Hay S A B C F E = S A D C F E
Cho hình bình hành ABCD,, phân giác góc A cắt đường chéo BD tại E và phân giác góc B cắt đường chéo AC tại F. Chứng minh rằng EF // AB.
Cho hình bình hành ABCD. Đường phân giác của các góc A và C cắt đường chéo BD tại E và F
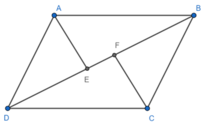
A. S A B C F E = 2 S A D C F E
B. S A B C F E < S A D C F E
C. S A B C F E = S A D C F E
D. S A B C F E > S A D C F E
Cho hình bình hành ABCD. Đường phân giác của các góc A và C cắt đường chéo BD tại E, F. Các hình đó có phải là đa giác lồi không? Vì sao?
Bài 1: Cho hình bình hành ABCD , đường chéo BD . Kẻ AH và CK vuông góc với BD tại H và K . Chứng minh tứ giác AHCK là hình bình hành. Bài 2: Cho hình bình hành ABCD có M N, lần lượt là trung điểm của AB CD , . AN và CM cắt BD lần lượt tại E và F . a) Chứng minh AMCN là hình bình hành. ( Hình 6) b) Từ F kẻ đường thẳng song song với AB cắt AN tại G. Chứng minh BF FE ED . Bài 3: Cho tam giác ABC cân tại A , lấy điểm D trên cạnh AB , điểm E trên cạnh AC sao cho BD CE . a) Tứ giác BDEC là hì gì? Vì sao? b) Các điểm D E, ở vị trí nào thì BD DE EC
Cho hình bình hành ABCD. Các tia phân giác của các góc A và ccắt đường chéo BD theo thứ tự tại các điểm E và F. Chứng minh:
a) SABCFE = SADCFE; b) SABCE = SADCF
Trên hình vẽ bên dưới, các tứ giác ABCD, EFCH đều là hình bình hành. Điểm E nằm trên đường chéo AC. Chứng minh rằng đa giác AEHD và hình ABCFE có diện tích bằng nhau
cho hình hành ABCD. Hai đường chéo AC và BD cắt nhau tại O. Từ A và C vẽ các đường thẳng vuông góc AE, CF xuống BD (E,F thuộc BD
a) so sánh OE và OF
b) chứng minh tứ giác AECF là hình bình hành
cho hình bình hành ABCD kẻ các đường phân giác góc A và D . Các đường phân giác cắt đường chéo BD và AC lần lượt tại M và N .Chứng minh MN //AD