Ta có:
△ ABC = △ CDA (c.c.c) ⇒ S A B C = S C D A (1)
△ EFC = △ CHE (c.c.c) ⇒ S E F C = S C H E (2)
Từ (1) và (2) ⇒ S A B C - S E F C = S C D A - S C H E
Hay S A B C F E = S A E H D

Ta có:
△ ABC = △ CDA (c.c.c) ⇒ S A B C = S C D A (1)
△ EFC = △ CHE (c.c.c) ⇒ S E F C = S C H E (2)
Từ (1) và (2) ⇒ S A B C - S E F C = S C D A - S C H E
Hay S A B C F E = S A E H D
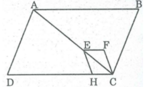
Trên hình vẽ bên dưới, các tứ giác ABCD, EFCH đều là hình bình hành. Điểm E nằm trên đường chéo AC. ABCFE có phải là đa giác lồi không? Vì sao?
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Trên AB lấy điểm E, trên CD lấy điểm F sao cho AE = CF.
a) Chứng minh: tam giác AEO = tam giác CFO
b) Chứng minh: E và F đối xứng nhau qua O.
c) Từ E vẽ Ex // AC cắt BC tại I, vẽ Fy // AC cắt AD tại K.
Chứng minh rằng: Tứ giác KEIF là hình bình hành.
Cho hình bình hành ABCD. Đường phân giác của các góc A và C cắt đường chéo BD tại E, F. Chứng minh hai hình ABCFE và ADCFE có cùng diện tích.
Cho hình bình hành ABCD vẽ đường thẳng xy qua A không cắt đường chéo BD. Gọi E là 1 điểm trên xy, E nằm ngoài hình bình hành ABCD. Chứng minh diện tích tam giác AEC = diện tích tam giác ABE + diệm tích tam giác ADE.
Giúp mình nhanh nhé !Cảm ơn các bạn nhiều !
Bài 1: Cho tam giác nhọn ABC có BC = 2AB. Lấy điểm D sao cho ABCD là hình bình hành. Gọi E là hình chiếu của C trên AB, M là trung điểm của AD. Chứng minh rằng góc BAD = 2 x góc AEM
Bài 2. Chứng minh rằng trong một tứ giác, đoạn thẳng nối trung điểm hai đường chéo và các đoạn thẳng nối trung điểm các cạnh đối của tứ giác đồng quy.
Bài 3. Cho điểm D nằm trong tam giác ABC. Vẽ các tam giác đều BDE, CDF (E, D, F nằm cùng phía đối với BC). Biết rằng tứ giác AEDF là hình bình hành. Chứng minh rằng
a) góc BDC = góc BEA và tam giác BDC = tam giác BEA.
b) Tam giác ABC là tam giác đều.
Giúp mik với nha !!! Tí nữa mik cần gấp rồi !!!
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Vẽ hình vuông AHIK (điểm H nằm giữa hai điểm C và I), hai đường thẳng KI và AB cắt nhau tại D.
a) Chứng minh rằng AD = AC.
b) Vẽ hình bình hành ADEC có hai đường chéo cắt nhau tại O, chứng minh rằng ba điểm O, H, K cùng nằm trên đường trung trực của đoạn AI và tứ giác KOEI là hình thang.
Biết rằng các đường chéo AC, BD chia ABCD thành 2 tam giác có diện tích bằng nhau. Chứng minh rằng ABCD là hình bình hành
5) Trên cạnh AB và CD của hình bình hành ABCD lần lượt lấy hai điểm M và N sao cho AM = CN, P là điểm trên AD, các đường thẳng MN, BP, CP chia hình bình hành thành ba tam giác và ba tứ giác. Chứng minh rằng trong đó diện tích một tam giác bằng tổng diện tích hai tam giác còn lại, và diện tích một tứ giác bằng tổng diện tích hai tứ giác còn lại.
Hình bình hành ABCD có 4 đỉnh lần lượt nằm trên các cạnh tứ giác EFGH, trong đó có 2 điểm là trung điểm của 2 cạnh tứ giác. Chứng minh diện tích hình bình hành ABCD = \(\frac{1}{2}\)diện tích tứ giác EFGH