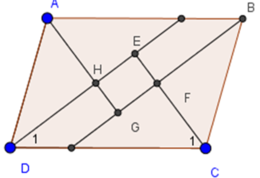
Ta có: ABCD là hình bình hành ( gt )
\(\Rightarrow\widehat{DAB}=\widehat{DCB};\widehat{ADC}=\widehat{ABC}\)
Dùng định lý tổng 4 góc trong tứ giác ABCD ta có:
\(\widehat{DAB}+\widehat{DCB}+\widehat{ADC}+\widehat{ABC}=360^0\)
Từ 2 điều trên suy ra \(\widehat{DAB}+\widehat{ABC}=\frac{360^0}{2}=160^0\)
Mà AG là tia phân giác của \(\widehat{DAB}\left(gt\right)\)
Áp dụng tính chất tia phân giác nên: \(\widehat{BAG}=\frac{1}{2}\widehat{DAB}\)
Tượng tự ta có: \(\widehat{ABG}=\frac{1}{2}\widehat{ABC}\) ( Vì BG là tia phân giác góc ABC )
Tiếp tục xét tam giác ABG rồi dùng định lý tổng 3 góc trong 1 tam giác = 180 độ là ra
Bài này có trong sách giáo khoa nè
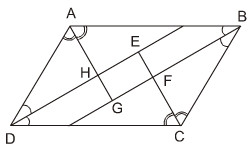
Vì ABCD là hình bình hành ( GT)
\(\Rightarrow\widehat{A}=\widehat{C}\) và \(\widehat{B}=\widehat{D}\)( tính chất hình bình hành)
Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\) ( tính chất ...)
\(\Rightarrow\widehat{A}+\widehat{B}=\frac{360^o}{2}=180^o\)
Ta lại có : \(\widehat{BAG}=\frac{1}{2}\widehat{A}\)( vì phân giác góc A )
và \(\widehat{ABG}=\frac{1}{2}\widehat{B}\) ( vì phân giác góc B )
\(\Leftrightarrow\widehat{BAG}+\widehat{ABG}=\frac{1}{2}\left(\widehat{A}+\widehat{B}\right)\)
\(=\frac{1}{2}.180^o=90^o\)
Xét tam giác AGB ta có :
\(\widehat{ABG}+\widehat{BAG}=90^o\)(1)
Lại có : \(\widehat{BAG}+\widehat{ABG}+\widehat{AGB}=180^o\) ( tổng 3 góc 1 tam giác) (2)
Từ (1) và (2)
\(\Rightarrow\widehat{AGB}=90^o\)
Xét tam giác DEC có:
\(\widehat{D}_1=\widehat{D}_2=\frac{\widehat{D}}{2}\) ( vì phân giác ...)
\(\widehat{C}_1=\widehat{C}_2=\frac{\widehat{C}}{2}\)( p/giác)
Lại có : \(\widehat{D}+\widehat{C}=180\)( trong cùng phía)
\(\Rightarrow\widehat{D}_1+\widehat{C_1}=\frac{180}{2}=90\)
\(\Rightarrow\widehat{E}_1=180-\left(D_1+\widehat{C}_1\right)=90\)
Bây giờ bạn chứng minh tương tự như trên góc EGH=90 độ nữa là ok .
Sau đó bạn kết luận tứ giác có 3 góc vuông là hình chữ nhật .
+ ABCD là hình bình hành
=> AB // CD
\(\Rightarrow\widehat{DAB}+\widehat{ADC}=180^o\)
( Hai góc trong cùng phía bù nhau )
AH là tia phân giác của \(\widehat{DAB}\)
\(\Rightarrow\widehat{DAH}=\frac{1}{2}.\widehat{DAB}\)
DH là tia phân giác của \(\widehat{ADC}\)
\(\Rightarrow\widehat{HDA}=\frac{1}{2}.\widehat{ADC}\)
\(\Delta ADH\)có :
\(\widehat{DAH}+\widehat{HDA}=\frac{1}{2}.\widehat{DAB}+\frac{1}{2}.\widehat{ADC}\)
\(=\frac{1}{2}.\left(\widehat{DAB}+\widehat{ADC}\right)=\frac{1}{2}.180^o=90^o\)
\(\Rightarrow\widehat{AHD}=90^o\Rightarrow\widehat{EHG}=\widehat{AHD}=90^o\)
( Hai góc đối đỉnh )
Chứng minh tương tự , ta được :
\(\widehat{HGF}=90^o\)và \(\widehat{GFE}=90^o\)
Vậy tứ giác EFGH là hình chữ nhật