cho hình bình hành ABCD ( AC lớn BD ) . kẻ CE vuông góc với đường thẳng AB tại E , CF vuông góc với AD tại F , BH vuông góc với đường thẳng AC tại H . gọi Q , K thứ tự là giao điểm của tia BH với các đường thẳng CD và AD . biết BC cắt HE ở i chứng minh : 1) tam giá ABH đồng dạng với ACE và AB nhân AE = AH nhân AC 2) tam giác IEB đồng dạng tam giác ICH 3) BH nhân BH = HK nhân HQ
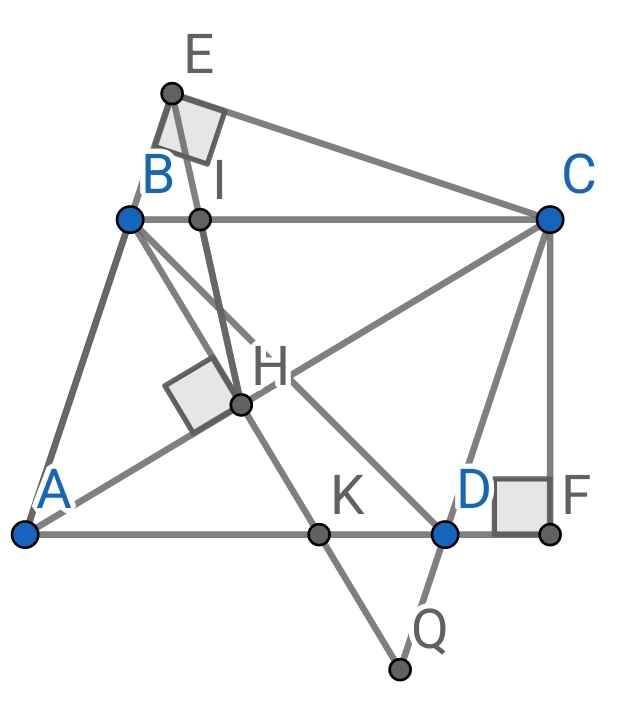
1) Xét hai tam giác vuông: ∆ABH và ∆ACE có:
∠A chung
∆ABH ∽ ∆ACE (g-g)
 ⇒ AB.AE = AH.AC
⇒ AB.AE = AH.AC
b) Sửa đề: ∆IBE ∽ ∆ICH
∆ACE vuông tại E
⇒ ∠BCE + ∠BCA = 90⁰
⇒ ∠BCE + ∠ICH = 90⁰
∆BCE vuông tại E
⇒ ∠BCE + ∠CBE = 90⁰
⇒ ∠BCE + ∠IBE = 90⁰
Mà ∠BCE + ∠ICH = 90⁰ (cmt)
⇒ ∠IBE = ∠ICH
Xét ∆IBE và ∆ICH có:
∠BIE = ∠CIH (đối đỉnh)
∠IBE = ∠ICH (cmt)
⇒ ∆IBE ∽ ∆ICH (g-g)
c) Do ABCD là hình bình hành (gt)
⇒ AB // CD và AD // BC
⇒ AB // CQ
Theo hệ quả của định lý Thales
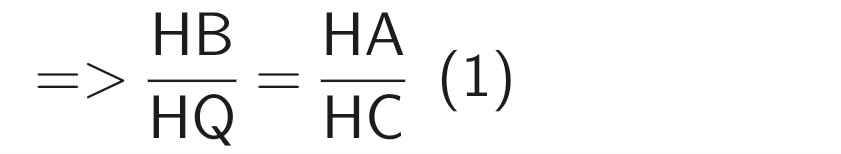
Do AD // BC (cmt)
⇒ AK // BC
Theo hệ quả của định lý Thales
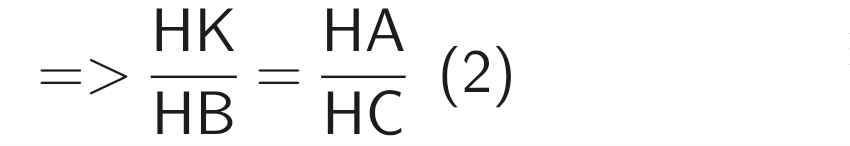 Từ (1) và (2)
Từ (1) và (2)
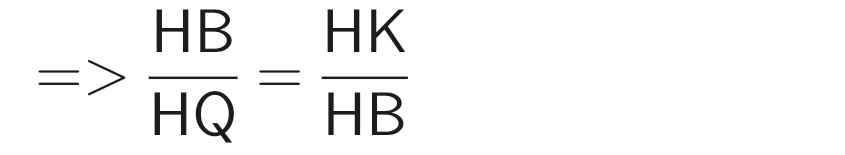 ⇒ HB.HB = HK.HQ
⇒ HB.HB = HK.HQ
Hay BH.BH = HK.HQ













