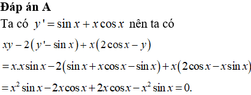Các câu hỏi tương tự
Cho các mệnh đề sau đây:(1) Hàm số
f
(
x
)
log
2
2
x
-
log
2
x
4
+
4
có tập xác định
D
[
0
;
+
∞
)
(2) Hàm số
y
log
a
x
có tiệm cận ngang(3) Hàm số
y
log
a
x
;
...
Đọc tiếp
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
Cho hàm số
y
s
i
n
x
+
c
o
s
x
+
2
. Mênh đề nào dưới đây đúng? A. Hàm số đạt cực đại tại các điểm
x
−
3
π
4
+
k
2
π
,
k
∈
ℤ
B. Hàm số đạt cực tiểu tại các điểm ...
Đọc tiếp
Cho hàm số y = s i n x + c o s x + 2 . Mênh đề nào dưới đây đúng?
A. Hàm số đạt cực đại tại các điểm
x = − 3 π 4 + k 2 π , k ∈ ℤ
B. Hàm số đạt cực tiểu tại các điểm
x = − π 4 + k 2 π , k ∈ ℤ
C. Hàm số đạt cực đại tại các điểm
x = π 4 + k 2 π , k ∈ ℤ
D. Hàm số đạt cực tiểu tại các điểm
x = π 4 + k 2 π , k ∈ ℤ
Cho các hàm số:
y
cos
x
,
y
sin
x
,
y
tan
x
,
y
c
o
t
x
.Trong các hàm số trên, có bao nhiêu hàm số chẵn? A. 1 B. 3 C. 2 D. 4
Đọc tiếp
Cho các hàm số: y = cos x , y = sin x , y = tan x , y = c o t x .
Trong các hàm số trên, có bao nhiêu hàm số chẵn?
A. 1
B. 3
C. 2
D. 4
Giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số
y
sin
x
+
2
cos
x
+
1
sin
x
+
cos
x
+
2...
Đọc tiếp
Giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = sin x + 2 cos x + 1 sin x + cos x + 2 là
A. m = - 1 2 ; M = 1
B. m = 1 ; M = 2
C. m = - 2 ; M = 1
D. m = - ; M = 2
Tìm đạo hàm y' của hàm số y = sin x + cos x
A. y' = 2cosx
B. y' = 2sinx
C. y' = sinx - cosx
D. y' = cosx - sinx
Cho
x
,
y
∈
0
;
π
2
thỏa cos 2x + cos 2y + 2 sin(x + y) 2Tìm giá trị nhỏ nhất của
P
sin
4
x
y
+
cos
4
y
x
A. ...
Đọc tiếp
Cho x , y ∈ 0 ; π 2 thỏa cos 2x + cos 2y + 2 sin(x + y) = 2Tìm giá trị nhỏ nhất của P = sin 4 x y + cos 4 y x
A. m i n P = 3 π
B. m i n P = 2 π
C. m i n P = 2 3 π
D. m i n P = 5 π
Tìm GTLN và GTNN của hàm số
y
sin
x
+
2
cos
x
+
1
sin
x
+
cos
x
+
3
(*) A.
m
a
x
y
4...
Đọc tiếp
Tìm GTLN và GTNN của hàm số y = sin x + 2 cos x + 1 sin x + cos x + 3 (*)
A. m a x y = 4 7 , m i n y = - 4 7
B. m a x y = 2 7 7 , m i n y = - 2 7 7
C. m a x y = 7 2 , m i n y = - 2 7
D. m a x y = 2 7 7 , m i n y = - 2 7 7
Đường thẳng
d
:
y
x
-
3
cắt đồ thị (C) của hàm số
y
x
+
1
x
-
2
tại hai điểm phân biệt A và B phân biệt. Gọi
d
1
,
d
2
lần lượt là khoảng cách từ A và B đến đường th...
Đọc tiếp
Đường thẳng d : y = x - 3 cắt đồ thị (C) của hàm số y = x + 1 x - 2 tại hai điểm phân biệt A và B phân biệt. Gọi d 1 , d 2 lần lượt là khoảng cách từ A và B đến đường thẳng D: x-y=0. Tính d = d 1 + d 2
A. d = 3 2
B. d = 3 2 2
C. d = 6
D. d = 2 2
Tìm GTLN và GTNN của hàm số
y
2
sin
x
+
cos
x
+
3
2
cos
x
-
sin
x
+
4
là: A.
m
i
n
y...
Đọc tiếp
Tìm GTLN và GTNN của hàm số y = 2 sin x + cos x + 3 2 cos x - sin x + 4 là:
A. m i n y = - 3 2 - 1 , m a x y = 3 2 + 1
B. m i n y = - 3 2 - 1 , m a x y = 3 2 - 1
C. m i n y = - 3 2 , m a x y = 3 2 - 1
D. m i n y = - 3 2 - 2 , m a x y = 3 2 - 1