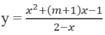Chọn C
Ta có y ' = - x 2 - m x - 2 . Hàm số nghịch biến trên khoảng (-∞; - 1) nếu y ' = - x 2 - m x - 2 ≤ 0 trên khoảng (-∞; -1)
Cách 1. Dùng định lí dấu của tam thức bậc hai. Ta có Δ = m 2 - 8
TH1: - 2 2 ≤ m ≤ 2 2 => Δ ≤ 0.
Lại có, hệ số a= -1 < 0 nên y' ≤ 0 ∀ x
Hàm số nghịch biến trên R
TH2: 
y' = 0. có hai nghiệm phân biệt là
Từ TH1 và TH2, ta có m ≤ 2 2
Cách 2. Dùng phương pháp biến thiên hàm số
Ta có
Từ đó suy ra
Do đó m ≤ 2 2
Vậy giá trị lớn nhất của tham số m để hàm số nghịch biến trên khoảng (-∞; -1) là m = 2 2
