Các câu hỏi tương tự
Cho hàm số y=x²-mx-3(1) a/Tìm m để đồ thị hàm số (1) cắt Õ tại điểm có hoành độ bằng 3 b/lập bảng biến thiên và vẽ đồ thị khi m=-2 c/Tìm tọa độ giao điểm (P) với đường thẳng (d)y=2x+9 d/tìm m để parabol của hàm số có đỉnh nằm trên trục Ox
Cho hàm số y=x²-2-3x,đồ thị là parabol(P) a/Xác định tọa độ đỉnh,trục đối xứng.Lập bảng biến thiên và vẽ đồ thị b/gọi A là điểm thuộc(P) và có hoành độ bằng 5. Tìm phương trình đường thẳng (d) đi qua 2 điểm A,I
Trong mặt phẳng Oxy cho đường thẳng Δ là đồ thị của hàm số: y 1/2x.a) Tìm tung độ của hai điểm Mo và M nằm trên Δ, có hoành độ lần lượt là 2 và 6.b) Cho vectơ u→ (2; 1). Hãy chứng tỏ cùng phương với u→.
Đọc tiếp
Trong mặt phẳng Oxy cho đường thẳng Δ là đồ thị của hàm số: y = 1/2x.
a) Tìm tung độ của hai điểm Mo và M nằm trên Δ, có hoành độ lần lượt là 2 và 6.
b) Cho vectơ u→ = (2; 1). Hãy chứng tỏ 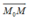 cùng phương với u→.
cùng phương với u→.
Cho hàm số
y
x
-
x
. Trên đồ thị của hàm số lấy hai điểm A và B hoành độ lần lượt là - 2 và 1. Phương trình đường thẳng AB là: A. B. C. D.
Đọc tiếp
Cho hàm số y = x - x . Trên đồ thị của hàm số lấy hai điểm A và B hoành độ lần lượt là - 2 và 1. Phương trình đường thẳng AB là:
A. 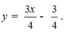
B. 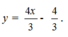
C. 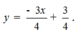
D. 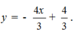
Gọi (P) là đồ thị hàm số
y
a
x
2
+
c
. Để đỉnh của (P) có tọa độ (0; -3) và một trong hai giao điểm của (P) với trục hoành là điểm có hoành độ bằng -5 thì: A.
a
3
25
,
c
3
B.
a
-...
Đọc tiếp
Gọi (P) là đồ thị hàm số y = a x 2 + c . Để đỉnh của (P) có tọa độ (0; -3) và một trong hai giao điểm của (P) với trục hoành là điểm có hoành độ bằng -5 thì:
A. a = 3 25 , c = 3
B. a = - 3 25 , c = - 3
C. a = - 3 25 , c = 3
D. a = 3 25 , c = - 3
Đồ thị hàm số có trục đối xứng là đường thẳng x=3, cắt trục tung tại điểm có tung độ bằng -16 và một trong hai giao điểm với trục hoành có hoành độ là -2. Tìm công thức của hàm số bậc hai.
Cho hàm số bậc nhất y ax + b. Tìm a và b, biết rằng đồ thị hàm số đi qua điểm M (−1; 1) và cắt trục hoành tại điểm có hoành độ là 5. A.
a
1
6
;
b
5
6
B.
a
−
1
6
;
b
−
5
6
C.
a
1
6...
Đọc tiếp
Cho hàm số bậc nhất y = ax + b. Tìm a và b, biết rằng đồ thị hàm số đi qua điểm M (−1; 1) và cắt trục hoành tại điểm có hoành độ là 5.
A. a = 1 6 ; b = 5 6
B. a = − 1 6 ; b = − 5 6
C. a = 1 6 ; b = − 5 6
D. a = − 1 6 ; b = 5 6
Cho hàm số với tham số m:
y
x
2
-
(
m
+
1
)
x
+
1
-
m
2
.Đồ thị hàm số đã cho cắt trục hoành tại hai điểm A, B sao cho gốc tọa độ O ở giữa A và B, đồng thời OB2OA khi: A. m 1 B.
m
-
1
2
C. m -1 D. m -3
Đọc tiếp
Cho hàm số với tham số m: y = x 2 - ( m + 1 ) x + 1 - m 2 .
Đồ thị hàm số đã cho cắt trục hoành tại hai điểm A, B sao cho gốc tọa độ O ở giữa A và B, đồng thời OB=2OA khi:
A. m = 1
B. m = - 1 2
C. m = -1
D. m = -3
1) Cho hàm số: yx^2-3x+4 có đồ thị là P và đường thẳng d có phương trình:y2x-m, và m là tham số. Tìm các giá trị của m để d cắt P tại hai điểm phân biệt A,B sao cho: OA^2+OB^257 và khi đó O là toa độ góc2) Cho hàm số fleft(xright)sqrt{3-x}-sqrt{3+x}-x^3-x. Tìm tất cả giá trị của tham số a để tập nghiệm của bất phương trình fleft(2x-1right)fleft(-2aright) có ít nhất là 3 số nguyên
Đọc tiếp
1) Cho hàm số: \(y=x^2-3x+4\) có đồ thị là P và đường thẳng d có phương trình:
\(y=2x-m\), và m là tham số. Tìm các giá trị của m để d cắt P tại hai điểm phân biệt \(A,B\) sao cho: \(OA^2+OB^2=57\) và khi đó O là toa độ góc
2) Cho hàm số \(f\left(x\right)=\sqrt{3-x}-\sqrt{3+x}-x^3-x\). Tìm tất cả giá trị của tham số a để tập nghiệm của bất phương trình \(f\left(2x-1\right)>f\left(-2a\right)\) có ít nhất là 3 số nguyên






