Các câu hỏi tương tự
Cho hàm số y f(x) liên tục trên
ℝ
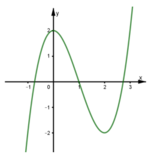
và có đồ thị như hình Gọi m là số nghiệm của phương trình f(f(x)) 1 . Khẳng định nào sau đây là đúng? A.
m
1
B.
m
0
C.
m
≤
0
D.
0
m
1
Đọc tiếp
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình
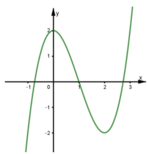
Gọi m là số nghiệm của phương trình f(f(x)) = 1 . Khẳng định nào sau đây là đúng?
A. m > 1
B. m > 0
C. m ≤ 0
D. 0 < m < 1
Cho hàm số yf(x) và yg(x) là hai hàm liên tục trên
ℝ
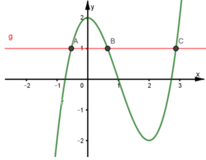
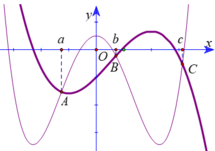
có đồ thị hàm số y f (x) là đường cong nét đậm và y g(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A,B,C của yf (x) và yg(x) trên hình vẽ lần lượt có hoành độ a.b.c. Tìm giá trị nhỏ nhất của hàm số h(x) f(x) - g(x) trên đoạn [a;c]?
Đọc tiếp
Cho hàm số y=f(x) và y=g(x) là hai hàm liên tục trên ℝ có đồ thị hàm số y = f '(x) là đường cong nét đậm và y = g(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A,B,C của y=f '(x) và y=g'(x) trên hình vẽ lần lượt có hoành độ a.b.c. Tìm giá trị nhỏ nhất của hàm số h(x) = f(x) - g(x) trên đoạn [a;c]?
![]()
![]()
![]()
![]()
Cho hàm số y f(x) liên tục trên
ℝ
{1} và có bảng biến thiên như sau: Đồ thị hàm số
y
1
2
f
(
x
)
+
3
có bao nhiêu đường tiệm cận đứng? A. 1 B. 2 C. 0 D. 2
Đọc tiếp
Cho hàm số y = f(x) liên tục trên ℝ \{1} và có bảng biến thiên như sau:
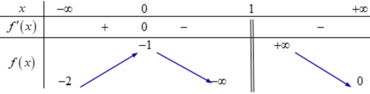 Đồ thị hàm số
y
=
1
2
f
(
x
)
+
3
có bao nhiêu đường tiệm cận đứng?
Đồ thị hàm số
y
=
1
2
f
(
x
)
+
3
có bao nhiêu đường tiệm cận đứng?
A. 1
B. 2
C. 0
D. 2
Cho hàm số f(x)liên tục trên đoạn [a ; b] và f(a) b, f(b) a, với 0 a b. Khi đó phương trình nào trong các phương trình sau đây luôn có nghiệm trên khoảng (a, b). A.
f
x
+
x
2
0
B.
f
x
+
a
0
C.
f
x
-
x
0
D.
f
x
+...
Đọc tiếp
Cho hàm số f(x)liên tục trên đoạn [a ; b] và f(a) = b, f(b) = a, với 0 < a < b. Khi đó phương trình nào trong các phương trình sau đây luôn có nghiệm trên khoảng (a, b).
A. f x + x 2 = 0
B. f x + a = 0
C. f x - x = 0
D. f x + x = 0
Cho hàm số
f
x
3
x
+
2
n
ế
u
x
-
1...
Đọc tiếp
Cho hàm số f x = 3 x + 2 n ế u x < - 1 x 2 - 1 n ế u x ≥ - 1
a. Vẽ đồ thị hàm số y= f(x). Từ đó nêu nhận xét vê tính liên tục của hàm số trên tập xác định của nó.
b. Khẳng định nhận xét trên bằng 1 chứng minh.
Trong mặt phẳng Oxy, cho phép biến hình f xác định như sau: Với mỗi M(x;y), ta có Mf(M) sao cho M(x;y) thỏa mãn xx;yax+by, với a,b là các hằng số thực. Khi đó a và b nhận giá trị nào trong các giá trị sau đây thì f trở thành phép biến hình đồng nhất? A. ab1 B. a0;b1 C. a0;b1 D. ab0
Đọc tiếp
Trong mặt phẳng Oxy, cho phép biến hình f xác định như sau: Với mỗi M(x;y), ta có M'=f(M) sao cho M'(x';y') thỏa mãn x'=x;y'=ax+by, với a,b là các hằng số thực. Khi đó a và b nhận giá trị nào trong các giá trị sau đây thì f trở thành phép biến hình đồng nhất?
A. a=b=1
B. a=0;b=1
C. a=0;b=1
D. a=b=0
Cho a,b,c,d là các số thực khác 0 và hàm số yf(x) asincx + bcosdx. Khẳng định nào sau đây là đúng? A. yf(x) asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi
c
d
là số hữu tỉ. B. yf(x) asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi
a
d
là số hữu tỉ. C. yf(x) asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi
c
b...
Đọc tiếp
Cho a,b,c,d là các số thực khác 0 và hàm số
y=f(x)= asincx + bcosdx. Khẳng định nào sau đây là đúng?
A. y=f(x)= asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi c d là số hữu tỉ.
B. y=f(x)= asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi a d là số hữu tỉ.
C. y=f(x)= asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi c b là số hữu tỉ.
D. y=f(x)= asincx + bcosdx là hàm số tuần hoàn khi và chỉ khi a x là số hữu tỉ.
Cho hàm số bậc ba
y
f
(
x
)
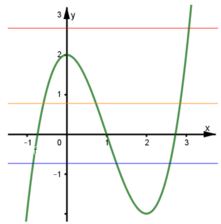
có đồ thị như hình vẽ bên. Tìm tham số m để hàm số
y
f
(
x
)
+
m
có ba điểm cực trị?
Đọc tiếp
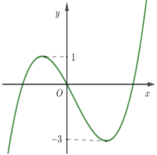
Cho hàm số bậc ba y = f ( x ) có đồ thị như hình vẽ bên. Tìm tham số m để hàm số y = f ( x ) + m có ba điểm cực trị?
![]()
![]()
![]()
![]()
cho đồ thị hàm số y=f(x),y=g(x) cùng tiếp xúc với đường thẳng (d):2x-y+1=0 tại M(1,3). Lập phương trình tiếp tuyến với đồ thị hàm số h(x)=f(x)*g(x)+2021x tại điểm có hoành độ bằng 1