Các câu hỏi tương tự
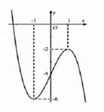
Cho hàm số y f(x) có đồ thị như hình vẽ bên.Số nghiệm của phương trình
2
f
x
−
1
−
3
0
là A. 1. B. 4. C. 3. D. 2.
Đọc tiếp
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
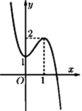
Số nghiệm của phương trình 2 f x − 1 − 3 = 0 là
A. 1.
B. 4.
C. 3.
D. 2.
Cho hàm số y f(x) có đồ thị như hình vẽ bên. Số nghiệm của phương trình
2
f
x
-
1
-
3
0
là: A. 1 B. 4 C. 3 D. 2
Đọc tiếp
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
Số nghiệm của phương trình 2 f x - 1 - 3 = 0 là:
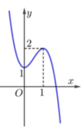
A. 1
B. 4
C. 3
D. 2
Cho hàm số y f(x) có đồ thị như hình vẽ bên. Số nghiệm của phương trình
2
f
x
-
1
-
3
0
là A. 1 B. 4 C. 3 D. 2
Đọc tiếp
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Số nghiệm của phương trình
2
f
x
-
1
-
3
=
0
là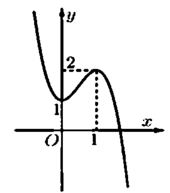
A. 1
B. 4
C. 3
D. 2
Cho hàm số y f(x) có đồ thị như hình vẽ bên. Số nghiệm của phương trình
2
f
x
−
1
−
3
0
là: A. 1 B. 4 C. 3 D. 2
Đọc tiếp
Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
Số nghiệm của phương trình 2 f x − 1 − 3 = 0 là:
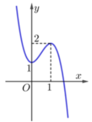
A. 1
B. 4
C. 3
D. 2
Cho hàm số f(x) có đồ thị như hình vẽ bên
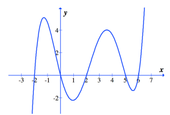
Số nghiệm của phương trình f(x)-2=0 là
A. 5.
B. 3.
C. 1.
D. 6.
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Phương trình f x = - 3 có số nghiệm là
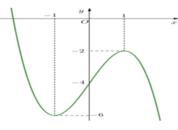
A. 0
B. 1
C. 2
D. 3
Cho hàm số
f
(
x
)
a
x
2
+
2
b
x
3
-
3
c
x
2
-
4
d
x
+
5
h
(a,b,c,d,hÎZ). Hàm số yf’(x) có đồ thị như hình vẽ bên. Tập nghiệm thực của phương trình f(x)5h có số phần tử bằng A. 3 B. 4 C. 2 D. 1
Đọc tiếp
Cho hàm số f ( x ) = a x 2 + 2 b x 3 - 3 c x 2 - 4 d x + 5 h (a,b,c,d,hÎZ). Hàm số y=f’(x) có đồ thị như hình vẽ bên. Tập nghiệm thực của phương trình f(x)=5h có số phần tử bằng
A. 3
B. 4
C. 2
D. 1
Cho hàm số y f(x) có đạo hàm liên tục trên R, đồ thị của hàm số y f′(x) như hình vẽ bên. Số nghiệm thực phân biệt của phương trình f(x) f(0) trên đoạn [−3;6] là A. 4 B. 3. C. 5. D. 2.
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên R, đồ thị của hàm số y = f′(x) như hình vẽ bên. Số nghiệm thực phân biệt của phương trình f(x) = f(0) trên đoạn [−3;6] là
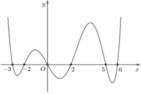
A. 4
B. 3.
C. 5.
D. 2.
Cho hàm số
f
(
x
)
ax
+
3
b
x
2
+
c
x
+
d
(
a
,
b
,
c
,
d
∈
R
)
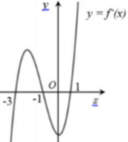
có đồ thị như hình vẽ sau. Số nghiệm của phương trình 4f(x) + 3 0 là A. 3 B. 2 C. 1 D. 0
Đọc tiếp
Cho hàm số f ( x ) = ax + 3 b x 2 + c x + d ( a , b , c , d ∈ R ) có đồ thị như hình vẽ sau. Số nghiệm của phương trình 4f(x) + 3 = 0 là
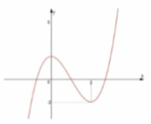
A. 3
B. 2
C. 1
D. 0