Đáp án C
f x = − x 3 − 3 x 2 + m ⇒ f ' x = − 3 x 2 − 6 x f ' x = 0 ⇔ x = 0 x = − 2 ( l o a i )
Tại x=0, ta có y 0 = m ⇒ y 0 = 0 ⇔ m = 0
Chọn phương án C.
Đáp án C
f x = − x 3 − 3 x 2 + m ⇒ f ' x = − 3 x 2 − 6 x f ' x = 0 ⇔ x = 0 x = − 2 ( l o a i )
Tại x=0, ta có y 0 = m ⇒ y 0 = 0 ⇔ m = 0
Chọn phương án C.
Cho hàm số y=f(x) liên tục, không âm trên R thỏa mãn f ( x ) . f ' ( x ) = 2 x f ( x ) 2 + 1 và f(0)=0. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y=f(x) trên đoạn [1;3] lần lượt là:
A. M=20;m=2
B. M = 4 11 ; m = 3
C. M = 20 ; m = 2
D. M = 3 11 ; m = 3
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau

Biết rằng f(0)+f(3)=f(2)+f(5) Giá trị nhỏ nhất, giá trị lớn nhất của hàm số f(x) trên đoạn [0;5] lần lượt là
A. f(0), f(5)
B. f(2), f(0)
C. f(1), f(5)
D. f(2), f(5)
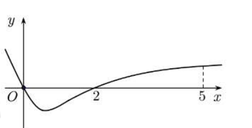
Cho hàm số f(x) có đạo hàm trên R và có đồ thị hàm y = f'(x) như hình vẽ. Biết rằng f ( 0 ) + f ( 3 ) = f ( 2 ) + f ( 5 ) . Giá trị nhỏ nhất và giá trị lớn của f(x) trên đoạn [0;5] lần lượt là:
A . f ( 2 ) ; f ( 0 )
B . f ( 0 ) ; f ( 5 )
C . f ( 2 ) ; f ( 5 )
D . f ( 1 ) ; f ( 3 )
Cho hàm số f(x) xác định trên R\{-1;1/2} và thỏa mãn f ' x = 4 x + 1 2 x 2 + x - 1 ; f 1 + f - 2 = 0 và f(0) + 2f(1)=0. Giá trị của biểu thức f(-3) + f(-3) + f(-1/2) bằng:
A. ln14+ln20-3/2ln10
B. -ln10
C.ln70
D. ln28
Cho hàm số y = f ( x ) = x - m 2 x + 4 với m là số thực. Tìm giá trị lớn nhất của m để hàm số f(x) có giá trị nhỏ nhất trên [0;1] bằng -1
A. m = 2
B. m = 0
C. m 6
D. m = 3
Cho hàm số f ( x ) = a x 4 + b x 2 + c có m i n ( - ∞ ; 0 ) f ( x ) = f ( - 1 ) . Giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [ 1 2 ;2] bằng
A. c + 8a
B. c - 7 16 a
C. c + 9 16 a
D. c - a
Cho hàm số y=f(x) có đạo hàm xác định trên tập R / - 1 và đồ thị hàm số y=f(x) như hình vẽ. Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị nhỏ nhất của hàm số y=f(sin2x) trên 0 ; π 2 . Tính P=m.M
A. P=0
B. P=8
C. P=12
D. P=4
Cho hàm số f(x)=3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 mf 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng (0;π/2). Số tập con của S bằng
A. 1
B. 2.
C. 4.
D. 16.
Cho hàm số f (x) có đạo hàm cấp hai liên tục trên đoạn [0;1] thoả mãn f ' ( x ) 2 + f x f ' ' x ≥ 1 ∀ m ∈ 0 ; 1 và f 2 0 + f 0 . f ' 0 = 3 2 Giá trị nhỏ nhất của tích phân ∫ 0 1 f 2 x d x bằng
A. 5 2
B. 1 2
C. 11 6
D. 7 2