Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
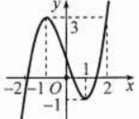
Cho hàm số yf(x) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(2sinx+1)m có nghiệm thuộc nửa khoảng
[
0
;
π
6
)
là A. (-2;0] B. (0;2] C. [-2;2] D. (-2;0)
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(2sinx+1)=m có nghiệm thuộc nửa khoảng [ 0 ; π 6 ) là
A. (-2;0]
B. (0;2]
C. [-2;2]
D. (-2;0)
Cho hàm số y f (x) liên tục trên
ℝ
và có đồ thị như hình vẽ bên.Tập hợp tất cả các giá trị thực của tham số m để phương trình f (sinx) m có nghiệm thuộc khoảng (0;
π
) là A. [-1;3) B. (-1;1) C. (-1;3) D. [-1;1 )
Đọc tiếp
Cho hàm số y = f (x) liên tục trên ℝ và có đồ thị như hình vẽ bên.
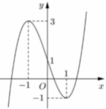
Tập hợp tất cả các giá trị thực của tham số m để phương trình f (sinx) = m có nghiệm thuộc khoảng (0; π ) là
A. [-1;3)
B. (-1;1)
C. (-1;3)
D. [-1;1 )
Cho hàm số y f(x) liên tục trên
ℝ
và có đồ thị như hình. Tập hợp tất cả các giá trị thực tham số m để phương trình f(cosx) m có 3 nghiệm phân biệt thuộc khoảng
(
0
;
3
π
2
]
là A. [-2;2] B. (0;2) C. (-2;2) D. (0;2]
Đọc tiếp
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình. Tập hợp tất cả các giá trị thực tham số m để phương trình f(cosx) = m có 3 nghiệm phân biệt thuộc khoảng ( 0 ; 3 π 2 ] là
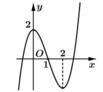
A. [-2;2]
B. (0;2)
C. (-2;2)
D. (0;2]
Cho hàm số yf(x) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(f(sinx))m có nghiệm thuộc khoảng
0
;
π
là A. [-1;3) B. (-1;1) C. (-1;3] D. [-1;1)
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(f(sinx))=m có nghiệm thuộc khoảng 0 ; π là
A. [-1;3)
B. (-1;1)
C. (-1;3]
D. [-1;1)
Cho hàm số yf(x) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sinx)m có nghiệm thuộc khoảng
0
;
π
là A. (-1;3) B. (-1;1) C. (-1;3) D. (-1;1)
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sinx)=m có nghiệm thuộc khoảng 0 ; π là
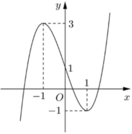
A. (-1;3)
B. (-1;1)
C. (-1;3)
D. (-1;1)
Cho hàm số yf(x) liên tục trên R và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(cosx)10 có 2 nghiệm phân biệt thuộc
(
0
;
3
π
2
]
là A. [-2;2] B. (0;2) C. (-2;2) D. [0;2)
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(cosx)=10 có 2 nghiệm phân biệt thuộc ( 0 ; 3 π 2 ] là
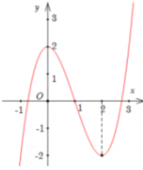
A. [-2;2]
B. (0;2)
C. (-2;2)
D. [0;2)
Cho hàm số f(x) liên tục trên và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình có nghiệm thuộc khoảng
(
0
;
π
)
là A. [-4;-2] B. [-4;0]{2} C. [-4;-2) D. (-4;-2]
Đọc tiếp
Cho hàm số f(x) liên tục trên và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình có nghiệm thuộc khoảng ( 0 ; π ) là
A. [-4;-2]
B. [-4;0]\{2}
C. [-4;-2)
D. (-4;-2]
Cho hàm số y f(x) liên tục trên R và có đồ thị như hình bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình
f
(
e
x
)
m
có nghiệm thuộc khoảng (0;ln3): A. (1;3) B.
-
1
3
;
0
C.
-
1...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f ( e x ) = m có nghiệm thuộc khoảng (0;ln3):
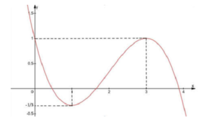
A. (1;3)
B. - 1 3 ; 0
C. - 1 3 ; 1
D. - 1 3 ; 1
Cho hàm số yf(x) liên tục trên R và có bảng biến thiên như hình vẽTập hợp tất cả các giá trị thực của tham số m để phương trình f(cos2x)-2m-10 có nghiệm thuộc khoảng
-
π
3
;
π
4
là A.
0
;
1
2...
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có bảng biến thiên như hình vẽ
Tập hợp tất cả các giá trị thực của tham số m để phương trình f(cos2x)-2m-1=0 có nghiệm thuộc khoảng - π 3 ; π 4 là
A. 0 ; 1 2
B. 0 ; - 1 2
C. 1 4 ; 1 2
D. - 10 ; 1 2