Đáp án là D.
Để đường thẳng y = 2 m - 1 cắt ( C ) tại hai điểm phân biệt thì 2 m - 1 = 5 2 m - 1 = 1 ⇔ m = 3 m = 1
Đáp án là D.
Để đường thẳng y = 2 m - 1 cắt ( C ) tại hai điểm phân biệt thì 2 m - 1 = 5 2 m - 1 = 1 ⇔ m = 3 m = 1
Cho hàm số y = f ( x ) liên tục trên R, có đồ thị (C) như hình bên. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = 2 m - 1 cắt đồ thị (C) tại 2 điểm phân biệt
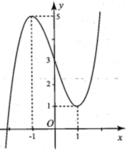
A. m > 3
B. m < 1
C. m = 1 m = 3
D. 1 < m < 3
Cho hàm số y = f(x)(x - 1) xác định và liên tục trên ℝ và có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = f x x − 1 cắt đồ thị hàm số tại 2 điểm có hoành độ nằm ngoài đoạn [-1;1]
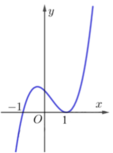
A. m > 0.
B. m > 1 m < 0 .
C. m < 1.
D. 0 < m < 1.
Cho hàm số y=f(x)(x-1) xác định và liên tục trên R và có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = m 2 - m cắt đồ thị hàm số f x x - 1 tại 2 điểm có hoành độ nằm ngoài đoạn [-1;1]
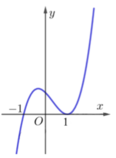
A. m > 0
B. [ m > 1 m < 0
C. m < 1
D. 0 < m < 1
Cho hàm số y=f(x) có đạo hàm liên tục trên ℝ . Hàm số y=f '(x) có đồ thị như hình vẽ bên dưới. Tìm tập hợp S tất cả các giá trị thực của tham số m để hàm số g x = 2 f 2 x + 3 f x + m có đúng 7 điểm cực trị, biết f a = 1 , f b = 0 , lim x → + ∞ f x = + ∞ , lim x → − ∞ f x = − ∞
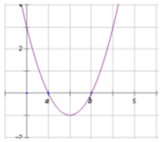
A. S = − 5 ; 0
B. S = − 8 ; 0
C. S = − 8 ; 1 6
D. S = − 5 ; 9 8
Cho hàm số y = f(x) liên tục trên
ℝ
và có đồ thị như hình dưới. Biết rằng trục hoành là tiệm cận ngang của đồ thị. Tìm tất cả các giá trị thực của tham số m để phương trình
f
x
=
4
m
+
2
log
4
2
có hai nghiệm phân biệt dương.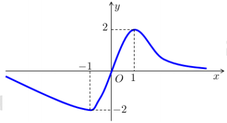
A. m > 1
B. 0 < m < 1
C. m < 0
D. 0 < m < 2
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình. Tập hợp tất cả các giá trị thực tham số m để phương trình f(cosx) = m có 3 nghiệm phân biệt thuộc khoảng ( 0 ; 3 π 2 ] là
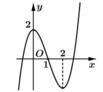
A. [-2;2]
B. (0;2)
C. (-2;2)
D. (0;2]
Cho hàm số y = 2 x - 1 x - 1 có đồ thị (C). Tìm tất cả các giá trị thực của tham số m để đường thẳng d: y = x + m cắt (C) tại hai điểm phân biệt A, B sao cho AB = 4
A. m = -1
B. [ m = 0 m = 3
C. [ m = - 1 m = 3
D. m = 4
Cho hàm số y = 2 x − 1 x − 1 có đồ thị (C). Tìm tất cả các giá trị thực của tham số m để đường thẳng d : y = x + m cắt (C) tại hai điểm phân biệt A, B sao cho AB = 4
A. m = − 1.
B. m = 0 m = 3 .
C. m = − 1 m = 3 .
D. m = 4.
Tìm tất cả các giá trị của tham số m để đường thẳng y = ( m - 1 ) x cắt đồ thị hàm số y = x 3 - 3 x 2 + m + 1 tại 3 điểm phân biệt A, B, C sao cho AB=BC
A. m ∈ ( - ∞ ; 0 ] ∪ [ 4 ; + ∞ )
B. m ∈ ( - 5 4 ; + ∞ )
C. m ∈ ( - 2 ; + ∞ )
D. m ∈ ℝ